You will write a program to generate a series of pseudo random numbers, using a linear feedback shift register method. You will start with an arbitrary number (not zero) x with a representation in n bits. If x = 15 and n = 4, then x = 1111. Then you will select a pair of bits, say bits 0 and 1, take their "xor" producing a new bit - in this case a 0. The number x will then shift to the right, with the new bit becoming the new high bit - in this case 0111. The process continues in this manner to produce a random set of bits. With four bits, we can only have up to 15 unique transitions before repetitions begin, or 2n - 1. With n = 32, the number of random bits has a much greater potential. The numbers actually produced by the "shifting" cannot be considered "random", since all but one of the bits overlap from each succeeding number. However, if we want to produce, say 100 6-bit numbers, then we need to shift the bits into an 6-bit register. We can then save its "value" in an array of 100 integers. Then we should produce the output which will display the distribution. Random numbers should follow a uniform
distribution. Using a 32-bit generator does not guarantee 2n - 1 random bits. For good results try using bit combinations 0/4, 0/7, 0/25, 0,26, 0/29.
Three random 4-bit numbers produced: 11, 13, 4, .... Try "tapping" different bit combinations, as well as the ones I suggested. To verify that the set of numbers you generated are really pseudo random, you will test them using the statistical χ2 test. You will generate 10,000 numbers in the 0-63 range. Then N=10,000 and r=64. You will then compute ∏2
by the formula
Example:
11001110 -> 11100111 -> 01110011 -> 10111001 -> 11011100 ->
11101110 -> 11110111 -> 01111011 -> 10111101 -> 01011110 -> etc
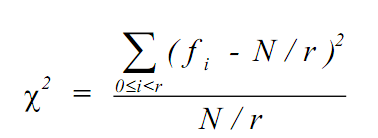
if χ2 is in the range of r ± 2 r , we conclude that distribution is indeed random. Otherwise it may not be. In your program, you will implement a random number generator module. Then the program will request 10,000 random numbers in the range of 0-25. It will then apply the test to
see if the numbers are random. You should apply the test a number of times because it has a 1/10 chance of showing failure even when the random distribution is successfully generated.
You will implement the random number generator as a RandonGenerator C++ class. The constructor will have to initialize the seed value. Subsequent calls to the random( ) method with integer parameter range will return a random value in the range between 0 to range-1 inclusive. The tapping bits should be set by default (in the constructor)