1. Ten turns of copper wire are to be wrapped helically around a cylinder of length 20mm and radius 2.5mm. The turns are to be wrapped evenly from one end of the cylinder to the other.
(a) Assume that the axis of the cylinder is on the +z-axis with the bottom at z = 0 and the top at z = 20. Find a

that describes the path ta.ken by the copper wire.
Hints: (1) You will need the parameterization formula for a helix discussed in class. (2) Since you want ten turns of wire, it is convenient to let the range of parameter t be 0 < t < 207r radians, which is ten complete 27r-radian circles.
(b) Use the arc length formula from section 9.5 along with your answer to part (a) to calculate the length of copper wire that will be required.
2. An object has velocity vector 6(0 that is described parametrically by 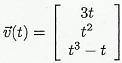
(a) Calculate the acceleration Ei(t) at time t = 1.
(b) Calculate the tangential (to the velocity) acceleration vector Ti at time t = 1.
(c) Calculate the normal (to the velocity) acceleration vector di at time t = 1.
3. Let a scalar function be defined as f(71 = 2xy - 3y2z.
(a) Calculate the gradient V f
(b) Solve for a unit-length vector that points in the direction of maximum increase of f at the point (x = 2, y = 1 z= 2)