Questions:
Two circles, A and B, touch each other at exactly one point...
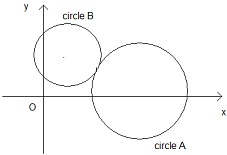
Two circles, A and B, touch each other at exactly one point, as shown in the diagram below. The equation of circle A is x2 - 18x + y2 - 2y + 46 = 0. Circle B has centre (1, k + 1) and radius 4.
a)i) Find the completed square form of x2 - 18x
Find the completed square form of y2 - 2y
ii) Use your answer from part i) to express the equation of circle A in the form
(x - a)2 + (y - b)2 = r2
iii) write down the centre and radius of circle A.
b)i) Explain why the distance between the centres of circles A and B is 10.
ii) Express this distance also in terms of k, and hence find the two possible values of k.
iii) Hence show that the two possible equations of circle B are
(x - 1)2 + (y-7)2 = 16 and (x-1)2 + (y+5)2 = 16
c) Show algebraically that the line y = 4/3 x - 1 is a tangent to circle A, and give the coordinates of the point of contact.
(You should work with fractions in this part of the question)