All locations are given with respect to a fixed-earth (geostationary) reference coordinate system located at the center of the earth. Distances are given in units of Earth Radii (ER) (using an average value of 1ER = 6,370km). Note that according to [1], GPS satellites are located at about 4.14ER from the center of the earth (20,000km above the earth's surface).
Use the notation Sl = (xl, yl, zl)T = position of lth Satellite, l = 1,.........4, S = (x, y, z)T = position of receiver (the Station to be tracked), Rl = true range to the receiver located at S from the satellite located at Sl, and �Sl = SSl = satellite-to-receiver distance vector.
For fixed satellite location, Sl, the true range, Rl, is a nonlinear function of the receiver location, S, and is given by,
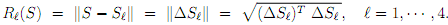
The pseudorange measurements are denoted by yl, and modeled as
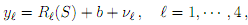
where the random noise term vl is i.i.d. with p.d.f. N(0, σ2). Further discussion of this model is given in the lecture supplement. The (constant) systematic clock bias error b is caused by an inaccurate clock in the GPS receiver. The number of range measurements taken to each satellite, m, is the same for each satellite.
�Knowing the satellite locations, Sl, l = 1,.........., 4, and having m pseudorange measurements, yl, to each of the l satellites, you are to estimate the receiver location, S, and the clock bias, b, using the Gradient Descent and Gauss methods for solving nonlinear least squares problems.
Write up your results using our standard format. Show and discuss the results of Steps 1-3 in some detail, including the observed convergence rates of steepest descent versus the Gauss-Newton method. Present plots showing the loss function l(k), receiver position estimate error || S'(k)-S|| in units of meters, and clock bias estimate error |b'(k) - b| also in units of meters, as a function of iteration step, k.