Assignment:
"Metcalfe's Law", which has been attributed to Bob Metcalfe (the inventor of Ethernet) says that the value of a network is proportional to the square of the number of users. The idea is that, if the value to each user of connecting to another user is $v, then as you add more users, the connections increase more rapidly than the users, so the value of the network with n users is v(n) = $v (n^2 - n)/2.
(a) On the graphs below, draw all the possible connections between the users. If the value of a connection is $v = $1, write the value of the network.
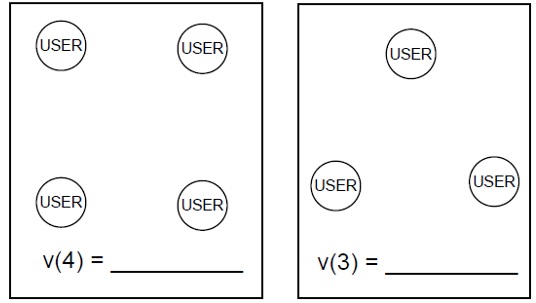
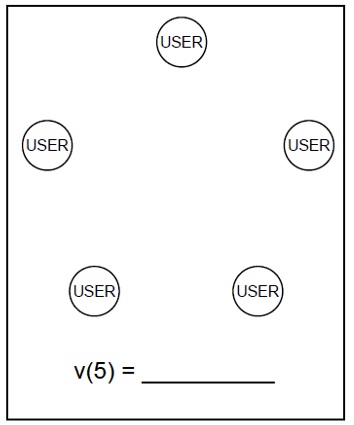
(b) What assumption will we usually make about network externalities which doesn't fit with Metcalfe's Law?