Questions:
Choose the one alternative that best completes the statement or answers the question.
Solve the problem.
1) Best Rentals charges a daily fee plus a mileage fee for renting its cars. Barney was charged $ 147 for 3 days and 300 miles, while Mary was charged $ 268 for 5 days and 600 miles. What does Best Rental charge per day and per mile?
A) $ 26 per day, 23¢ per mile B) $ 23 per day, 26¢ per mile
C) $ 25 per day, 24¢ per mile D) $ 27 per day, 24¢ per mile
Write an equation for the line. Use slope-intercept form, if possible.
2) Through ( 5, -6) and ( 0, -8)
A) y = 11/8x -8 B) y = -11/8x - 8
C) y = 2/5x - 8 D) y = -2/5x - 8
Use the echelon method to solve the system of two equations in two unknowns.
3) 5x - 7y = 8
3x - 4y = 5
A) ( 3, 2) B) ( 2, 2) C) ( 3, 1) D) No solution
Write the augmented matrix for the system. Do not solve.
4) -2x + 6y = 40
2x + 2y = 8
A)
B)
C)
D)
Find the slope of the line passing through the given pair of points.
5) ( 3, 2) and ( 3, 9)
A) Undefined B) - 7/6 C) 0 D) 11/6
Use the echelon method to solve the system of three equations in three unknowns.
6) x + y + z = 2
x - y + 5z = 0
4x + y + z = 14
A) ( -1, -1, 4) B) ( 4, -1, -1) C) ( -1, 4, -1) D) No solution
Find the slope of the line.
7) A line parallel to 4y - 5x = -7
A) 7/5 B) 5/4 C) 4/5 D) - 5/4
Use the echelon method to solve the system.
8) x/2 + y/2 = 0
x - y = -12
A) (-6,6) B) (6,7 ) C) (-7, 7 ) D) No solutuion
Solve the problem.
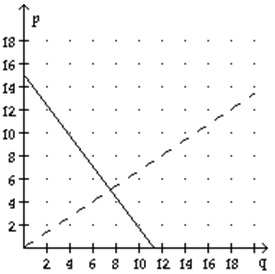
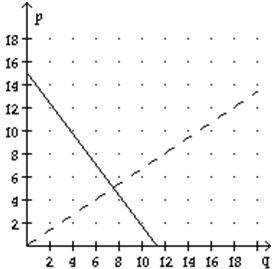
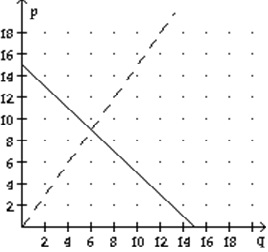
9) Let the supply and demand functions for a certain model of electric pencil sharpener be given by
p = S(q) = 2/3q and p = D(q) = 15 - 4/3q
where p is the price in dollars and q is the quantity of pencil sharpeners (in hundreds). Graph these functions on the same axes (graph the supply function as a dashed line and the demand function as a solid line). Also, find the equilibrium quantity and the equilibrium price.
A)
Equilibrium quantity: 750
Equililbrium price: $5
B)
Equilibrium quantity: 950
Equilibrium price: $7
C)
Equilibrium quantity: 900
Equilibrium price: $6.00
D)
Equilibrium quantity: 600
Equilibrium price: $9.00
Find the slope of the line.
10) A line parallel to -4x = 5y + 11
A) - 11/4 B) -5/4 C) -4/5 D) 4/5
Use the echelon method to solve the system of two equations in two unknowns.
11) x - 2y = -2
6x - 3y = -30
A) ( -6, -2) B) ( -7, -1) C) ( 6, -1) D) No solution
Provide an appropriate response.
12) Find k so that the line through (3, k) and (1, -2) is parallel to 5x - 3y= -2. Find k so that the line is perpendicular to 3x + 2y = 6 A) 4/3; -2/3 B) 16/3; -10/3 C) 4/3; -10/3 D) 16/3; -2/3
Write an equation for the line. Use slope-intercept form, if possible.
13) Through ( 4, 0), m = -1
A) y = x - 4 B) y = - 4x C) y = -x + 4 D) y = 4x
Write the augmented matrix for the system. Do not solve.
14) 4x - 2y = 14
-2y = -2
|
A)
|
14
|
-2
|
4
|
|
B)
|
-2
|
0
|
-2
|
|
C)
|
4
|
-2
|
14
|
|
D)
|
4
|
-2
|
14
|
|
|
-2
|
0
|
-2
|
|
|
4
|
-2
|
-2
|
|
|
0
|
-2
|
-2
|
|
|
-2
|
-2
|
0
|
Find the slope of the line passing through the given pair of points.
15) ( 5, 4) and ( 2, 2)
A) 2/3 B) 3/2 C) -2/3 D) 6/7
Use the Gauss-Jordan method to solve the system of equations.
16) 3x + 3y = -6
2x + 8y = 14
A) ( 3, -5) B) ( -5, -3) C) ( -5, 3) D) No solution
Write an equation for the line. Use slope-intercept form, if possible.
17) Through ( 3, 5), m = - 5/9
A) y = -5/9x + 5/3 B) y = 5/9x -20/3
C) y = 5/9x + 5/3 D) y = -5/9x + 20/3
Find the slope of the line.
18) 5x + 2y = 16
A) 8 B) 5/2 C) -5/2 D) 2/5
Use the echelon method to solve the system of two equations in two unknowns.
19) x + 3y = 9
-7x + 4y = 12
A) ( -3, 0) B) ( 1, 2) C) ( 0, 3) D) No solution
Find the slope of the line passing through the given pair of points.
20) ( 6, -4) and ( -7, 1)
A) - 5/13 B) -13/5 C) 5/13 D) 3