Assignment:
A navigator is sailing around the world, which we assume is equipped with a set of axes (x, y, z where2 points from the center of the earth to the north pole. The navigator does not know her location or what time it is. To determine these, she decides to use signals transmitted by four satellites. At time t, she records all four incoming signals. Each signal contains the location (x, y, z) of the satellite that sent it, together with the time τ at which this signal was sent (we assume that the satellites are perfectly synchronized.) The information she recorded is presented in Table 9.
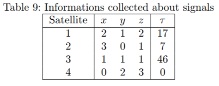
The signal sent by each satellite travels at the speed of light, which we assume here is 0.047 (in units of earth radii per millisecond)
1. What are the four unknows (variables) of this problem?
2. Write a system of four quadratic equations that these variables must satisfy.
3. From the system you wrote in Part 2, create a new system by subtracting the first one of your equations from each of the other three.
4. Use Gaussian elimination to obtain all solutions to the system you obtained in Part 3.
5. Use your derivations in Parts 2-4 above to determine the location of the navigator and the time at which she recorded the satellite signals.