Write a matlab code to visualize the bilinear functions n1

Question

Problem 1

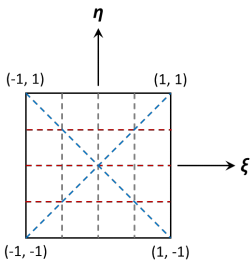
a. Write a MATLAB code to visualize the bilinear functions (N₁, N₂, N₃, N₄) of a 4-node quadrilateral element in the natural domain. In your code use the MATLAB function surf (or similar) to plot a 3D surface showing each of the shape functions. What value do you get when summing up all shape functions at every point of the domain?

b. Write a MATLAB code that transforms the straight lines illustrated in the Figure from the natural domain to the physical domain. (Note: A straight line in computer representation is a set of discrete points.) Assume an element in the physical domain with coordinates at: A(-3,-2), B(5,-1), C(3,4), D(-2, 2). Which lines remain straight after transformation?

Problem 2

Given the quadrilateral bilinear element in the physical domain where a is a parameter (the coordinates of node 3) ranging from ∞ ≤ α ≤ ∞:

a. Find |J| (the determinant of the Jacobian) at x = a and y = a as a function of the parameter a.

b. What is the condition that parameter α should satisfy for |J| > 0 everywhere within the element?

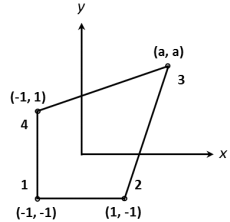
Explain how this relates to distorted elements.

For the next set of questions choose α = 2 and compute:

c. The value of N₂ at point (x = 0, y =-1).
d. The value of |J| at point (x = 0, y =-1).
e. The value of N_1,y at point (x = 0, y =-1).

Problem 3

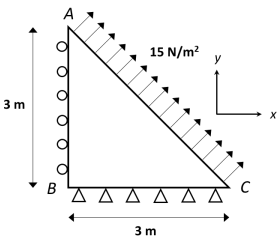
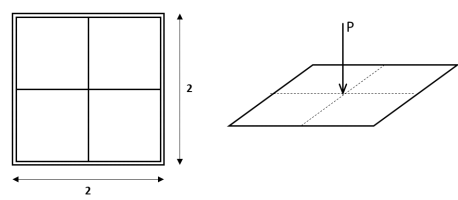
Consider the following membrane clamped at all 4 sides (a membrane can be modeled by Poisson's equation T.∇²u = f, where u is the transverse displacement and T is the tensile stiffness of the membrane). The membrane is discretized into 4 identical quadrilateral elements (4-node elements). Compute the displacement of the center point under an applied point force P = 10 and T = 1. The dimensions are given in the figure. Use hand calculations to solve the problem.

Bonus Problem

Consider the one element triangular mesh shown in the Figure. The boundary conditions are as follows. The edge BC is constrained in both x and y directions, whereas the edge AB is constrained in the x direction and traction-free in y. The edge AC is subjected to normal traction as shown. Assume plane strain conditions with Young's Modulus of E = 200GPa and Poisson's ratio  = 0:3.

a. Construct the global stiffness matrix.
b. Construct the global force vector.
c. Solve for the unknown displacements.
d. Calculate the stress and strain at point (1.5, 1.5).