What values of h doom the crop to complete depletion

Question

Separation of Variables, System Progress, and Phase Diagrams

Solve the following problems:

1.    Solve by separation of variables and plot the solution to the ODE: dx/dt =x^·

                        x^· =4x-2;t≥1,x(1)=3/4
                 
2.    Solve the equation  x^·= —x In (x), t ≥ 0, x(0)= x_0.

What is the asymtotic value of x at t-> ∞. EXPLAIN your answer.

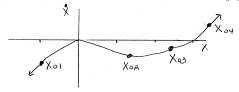
3.    For the given graph, re-sketch a graph for x₀₁ and indicate the system progress (using arrows and EXPLAIN) from x₀₁ as t-> ∞op. Identify any critical points as stable, unstable, or semi-stable (EXPLAIN). Repeat for X₀₂ x₀₃, and X₀₄.

4. Draw and label the phase diagram (x^· vs. x). Indicate the system progress (using arrows and EXPLAIN). Identify any critical points as stable, unstable, or semi-stable (EXPLAIN): x^· = a₁x - a₂, a₁, >0, a₂ >0.

5. Draw and label the phase diagram ((x^· vs. x) for x^· = 3x² - 9x. Indicate the system progress (using arrows and EXPLAIN). Identity any critical points as stable, unstable, or semi-stable (EXPLAIN).

6. A harvesting model is represented by: x^· = a₁x - a₂x² - h; a1 > 0, a2 > 0, h> 0.

a.    Draw the phase diagram ( (x^· vs.x) and label the values of the intercepts and the point of maximum x^·

b.    Identify any critical points as stable, unstable, or semi-stable (EXPLAIN).

c.    What values of h doom the crop to complete depletion (EXPLAIN)?

d.    What is the maximum value of h that produces a critical crop level (EXPLAIN).

e.    Plot x^· vs. x for maximum h and determine if the critical point is stable, unstable, or semi-stable (EXPLAIN).

f.    How does the maximum value of h change if a₁, the reproduction rate parameter, increases (EXPLAIN)?

g.    How does the maximum value of h change if a₁, the reproduction rate parameter, decreases (EXPLAIN)?

7.   x^· = a₁,x - a₂ If x has units of ounces and x^· has units of ounces per second, what are the units of a₁ and a₂ (EXPLAIN)?