Discuss the below:
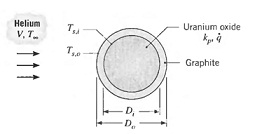
Q: A high-temperature gas reactor (HTGR) consists of spherical, uranium oxide fuel elements in which there is uniform volumetric heating (q). Each fuel element is embedded in a graphite spherical shell which is cooled by a helium gas flow at 1 atm.
Consider steady-state conditions for which radiation effects may be neglected, the gas velocity and temperature are V = 20 m/s and T8 = 500 K, the pellet and shell diameters are Di = 10 mm and Do = 12 mm, and the shell surface temperature is Ts.o = 1300 K. The uranium oxide and graphite each have a thermal conductivity of kp = kg = 2 W/m · K.
(a) What is the rate of heat transfer from a single pellet to the gas stream?
(b) What is the volumetric rate of heat generation in the pellet and what is the temperature at the pellet-graphite interface (Ts,i>?
(c) Obtain an expression for the radial temperature distribution T(r), in the pellet, expressing your result in terms of the temperature at the center of the pellet, T (0). Evaluate T (0) for the prescribed conditions.
(d) Determine Ts,o, Ts,i and T(0) as a function of the gas velocity for 5 <>< 20="" m/s="" and="" q="1.50" x="" 108="">