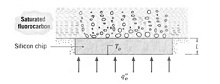
Solve the following problem:
Q: A silicon chip of thickness L = 2.5 mm and thermal conductivity ks = 135 W/m · K is cooled by boiling a saturated fluorocarbon liquid (Tsat = 57°C) on its surface. The electronic circuits on the bottom of the chip produce a uniform heat flux of q"o = 5 x 104 W/m2, while the sides of the chip are perfectly insulated. Properties of the saturated fluorocarbon are cp,l = 1100J/kg · K, hfg = 84,400Jlkg, p1= 1619.2 kg/m3, Pv = 13.4 kg/m3, s = 8.1 x 10-3 kg/s2, µ1 = 440 x 10-6 kg/m · s, and Pr1 = 9.01. In addition, the nucleate boiling constants are Cs,f = 0.005 and n = 1.7.
(a) What is the steady-state temperature To at the bottom of the chip? If, during testing of the chip, q"o is increased to 90% of the critical heat flux, what is the new steady-state value of To?
(b) Compute and plot the chip surface temperatures (top and bottom) as a function of heat flux for 0.20 < q"o/q"max="">< 0.90.="" if="" the="" maximum="" allowable="" chip="" temperature="" is="" 80?c,="" what="" is="" the="" maximum="" allowable="" value="" of="" q"o?="">