What is the rotational kinetic energy of the combination

Question

Assignment:

Problem 1. A mass m hangs vertically while attached to a rope that is wrapped around a wheel of mass M and radius R. The spokes on the wheel are so light that their mast can be neglected and the entire wheel can be treated as a hoop.

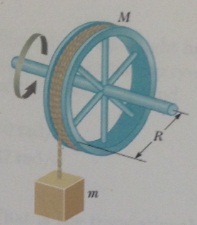
(a) Find an expression for the magnitude of the angular acceleration of the wheel

A. α = (m/m+M) (g/R)

B. α = (m/m +M/2) (g/R)

C. α = (3/4 m/m+M) (g/R)

D. α=  (m/m+M/2) g

(b) Find an expression for the magnitude of the Torque on the wheel

A. T = mgR

B. T= (M m/2m+M) g R

C. T = (M m/m+M/2) g R²

D. T= (M m/m+M) g R

(c) Find an expression for the speed of the mass m after it has descended a distance h

A. v = √2g h

B. v = (√m/m+M) (√2 gh)

C. v = (√m/m+M/2) (√2 gh)

D. v = (√m/m+M) (√gh)

Problem 2. A merry-go-round of radius R = 1.5 m has a moment of inertia of I = 175 kg m2. The merry go round is given an initial angular speed of 1.6 rad/s. Shortly after the merry go round begins rotating a cylindrical weight is dropped on the merry-go-round.

(a) The cylindrical weight has a mass of 120 kg and a radius of 0.50 m. Find the new angular speed of the merry-go-round if the cylinder is dropped in the middle (or center) of the merry-go-round.

A. 1.50 rad/s

B. 1.47 rad/s

C. 1.37 rad/s

D. 1.55 rad/s

(b) What is the translational speed of a point on the edge of the merry-go-round after the cylindrical mass has been dropped on the merry go round?

A. 0.74 m/s

B. 0.79 m/s

C. 2.21 m/s

D. 2.25 m/s

(c) What is the Rotational Kinetic Energy of the combination of the merry-go-round and cylindrical weight?

A. 191.2 J

B. 205.3 J

C. 213.6J

D. 224 J