What is the probability of one bullet missing guys head

Question

Assignment:

1) A chitauritwo (Loki's weird alien friends) is flying past Hawkeye who is stationed on top of a building. The trajectory of the chitauritwo is given by the equations

x_c = -100m + 1ms^-1t+(1/2)0.1t²

y_c = 100m

z_c = 440m

Hawkeye's position is given by x_c = 0, y_c = 0 and z_c = 440m. If he is to fire an arrow with an initial velocity of 137 m s^-1 at time t = 0, will he be able to shoot the chitauritwo? In what direction should he fire his arrow? Ignore air resistance, because the arrow is so fast, and note that gravity acts in the negative z-direction.

This is an intersection problem, so we have to write down the trajectory of the arrow and put the x-, y and z-coordinates of the arrow as a function of time equal to the x-, y- and z-coordinates of the chitauritwo (given in the problem).

i. You have the starting location of the arrow so write down the equation for the position of the arrow in the x-direction as a function of time (note there is no air resistance so no acceleration). Put this equal to the x-coordinate of the chitauritwo to obtain your first equation.

ii. Do the same as in i but in the y-direction (should be simpler as the chitauritwo doesn't move in this direction).

iii. Obtain a similar equation in the z-direction. This is height so Hawkeye will have to aim slightly upwards to overcome the effects of gravity, which will appear in this equation as a negative term.

So now you have three equations, but 4 unknowns! The unknowns are the initial velocity of the arrow (in x, y, and z) and time. But wait, we have a fourth equation.

iv. The magnitude of the velocity is dictated by the bow. The magnitude is 137 m s^-1. Therefore, Pythagoras theory gives us our fourth equation. 4 unknowns and 4 equations. Now its a math problem. Plug it into a calculator or a computer if you can't do the math.

2) Suppose that a planet were discovered between the sun and Mercury, with a circular orbit of radius equal to 2/3 of the average orbit radius of Mercury. (Such a planet was once postulated, in part to explain the precession of Mercury's orbit. It was even given the name Vulcan, although we now have no evidence that it actually exists. Mercury's precession has been explained by general relativity.) The orbital period of Mercury is 88.0 days.

What would be the orbital period of such a planet?

You shouldn't need any help with this question as its a simple application of Kepler's 3rd law.

3) A skier leaves the ramp of a ski jump with a velocity of 10 m/s at 20^o above the horizontal as shown. The slope where she will land is inclined downward at 40^o , and air resistance is negligible. Find the distance from the end of the ramp to where the jumper lands and her velocity components just before landing.

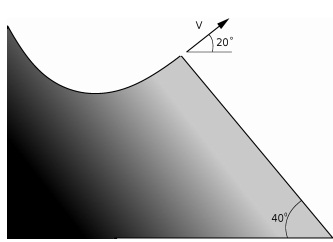
This is an interesting projectile motion problem, because the area where the projectile is landing (the projectile being the skier in this  problem) is inclined.

i. First you need to write down the equation of motion for the skier in the x-direction after she has left the ski jump. Take the edge of the ski jump to be x = 0 and y = 0, and the point of time when she leaves as t = 0.

ii. Write down the equation of motion for the skier in the y-direction. Don't forget gravity.

iii. You should now have two equations but three unknowns (the x and y distances when she lands on the slope and the time this took). The third equation comes from the slope itself! Given that the slope is going down at 40^o can you write an equation relating the x and y distances when she lands on the slope?

Now you have 3 equations and 3 unknowns it should be easy enough. Given this information you should be able to get the quantities asked for in the problem.

4) High jumpers usually sustain fractures in the lower third of the fibula. The world record for the high jump is held by Javier Sotomayor (Cuba) at 2.45 m (1993). If he weighed 68 kg could muster a run-up speed of 9 m s^-1, had a center of mass which was 1.2 m of the floor and took 0.3 s to push off from the floor then calculate the stress in his fibula. Note that during the Fosbury Flop the higher jumper pushes
of from the ground using both feet, the cross-sectional area of the fibula is 1 cm² , and that the fibula plays a minor role in weight-bearing with the tibia supporting approximately 95% of the weight. Stress is defined as force per unit area.

i. In order for Javier to make the jump how much energy does he need? Note he only has to raise his center of mass to 2.45 m from 1.2 m.

ii. By balancing potential energy and kinetic energy, how much velocity does he need?

iii. Given that it took an estimated 0.3 s for this velocity to be acquired, what was his acceleration and what is the force required to generate this acceleration.

iv. If the fibula only provides 5% of this force then how much force is that? And given the definition of stress, what is the stress in the fibula?

5) A shotgun fires a large number of pellets upward, with some pellets traveling very nearly vertically and others as much as 1.0^o from the vertical. Assume that the initial speed of the pellets is uniformly 150 m s^-1 and ignore air resistance. Within what radius from the point of firing will the pellets land? If there are 1000 pellets, and they fall in a uniform distribution over a circle with the radius you just calculated, what is the probability that at least one pellet will fall on the head of the person who fires the gun?

For this question you might need to brush up on your high school math. Hows your probability?

i. Use the range equation to find the furthest that a bullet could land.

ii. If 1000 bullets fall in a circle with this radius then we can find the probability of at least one bullet falling on the shooters head. First make up the area of his head, say, 0.01 m²? What is the probability of a single bullet hitting the guy?

iii. What is the probability of one bullet missing the guys head?

iv. What is the probability that all the bullets will miss?

v. What is the probability that not all of the bullets will miss, and that at least one will hit?

6) Consider the experiment shown below. A block is pulled across a flat but rough surface. The force applied to the block is plotted on the x-axis while the frictional force due to the surface of the block and the rough surface is plotted on the y-axis.

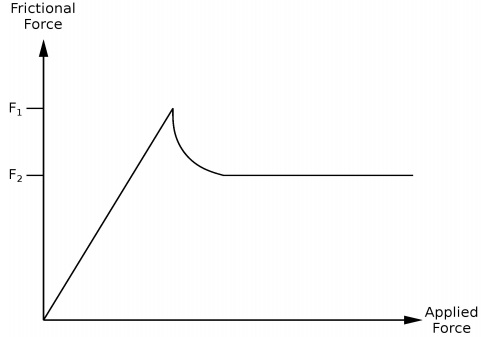
What is the value of the applied force when the frictional force is equal to F₁? Explain the features of the graph. Sketch a plot of the position of the block as a function of time, assuming the applied force ramps up linearly with time. Sketch a plot of the velocity of the block as a function of time, assuming the applied force ramps up linearly with time. Sketch a plot of the acceleration of the block as a function of time, assuming the applied force ramps up linearly with time.

There are some key words here. "Flat surface" implies that you can ignore gravity, but "rough surface" implies that friction is going to be important.

i. The first thing the problem asks is to give the value of the applied force when the frictional force is equal to F₁. As the static friction opposes the applied force, then the frictional force and applied force should be equal. The block isn't moving yet!

ii. You should be able to explain this graph. If not then consult your notes.

iii. You have to provide plots of position, velocity and acceleration. I would consider these in the reverse order. First what is the net force acting on the block as a function of time? Recall that the applied force is said to increase linearly with time. The acceleration is just proportional to the net force (applied force minus frictional force). Second, if you have acceleration as a function of time, then the integration of this would give you velocity. In other words, the velocity vs time plot is the area under the curve of the acceleration vs time graph. Thirdly, the position vs time is the area under the curve of the velocity vs time graph.