Solve the following problem:
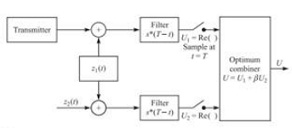
In the binary communication system shown in Figure ,z1(t) and z2(t) are statistically independent white Gaussian noise processes with zero-mean and identical autocorrelation functions Rzz(τ ) = 2N0δ(τ ). The sampled values U1 and U2 represent the real parts of the matched filter outputs. For example, if s1(t) is transmitted, then we have
U1 = 2ε + N1
U2 = N1 + N2
where ε is the transmitted signal energy and
Nk = Re[∫T0 s*1(t)zk(t)dt] , k = 1, 2
t is apparent that U1 and U2 are correlated Gaussian variables while N1 and N2 are independent Gaussian variables. Thus,
p(n1) = 1/√2πσ exp [-(n21/2σ2)]
p(n2) = 1/√2πσ exp [-(n22/2σ2)]
where the variance of Nk is σ2 = 2EN0.
a. Show that the joint probability density function for U1 and U2 is
p(u1, u2 ) = 1/2πσ2 exp { -(1/σ2)[u2 + 2ε)2 - u2(u1 - 2ε) + 1/2 u 2/2]}
if s(t) is transmitted and
p(u1, u2 ) = 1/2πσ2 exp { -(1/σ2)[u1 + 2ε)2 - u2(u1 + 2ε) + 1/2 u 2/2]}
if -s(t) is transmitted.
b. Based on the likelihood ratio, show that the optimum combination of U1 and U2 results in the decision variable
U = U1 + βU2
where β is a constant. What is the optimum value of β?
c. Suppose that s(t) is transmitted. What is the probability density function of U?
d. What is the probability of error assuming that s(t) was transmitted? Express your answer as a function for the SNR E/N0.
e. What is the loss in performance if only U = U1 is the decision variable?