Question 1. Math Review Question:
a. You are told that there are two linear relationships between Y and X where Y is the variable measured on the vertical axis and X is the variable measured on the horizontal axis. The first linear relationship is given by the equation Y = 50 – 2X.
You are told that the second linear relationship goes through the origin and that for every 1 unit increase in the X variable, the Y variable increases by 8 units.
What is the equation for the second line and what is the solution (X, Y) for your two equations?
b. You are told that there are two linear relationships between Y and X where Y is the variable measured on the vertical axis and X is the variable measured on the horizontal axis. The first linear relationship contains the points (125, 75) and (50, 150). The second linear relationship contains the points (50, 100) and (150, 150).
Find the equations for the two lines and then calculate the solution (X, Y) for these two equations.
c. You are told that there are two linear relationships between Y and X where Y is the variable measured on the vertical axis and X is the variable measured on the horizontal axis. The first linear relationship is described as follows: the Y variable is equal to 5 more than twice the X variable. The second linear relationship is described as follows: the X variable is equal to 5 less than twice the Y variable.
Find the equations for the two lines and then calculate the solution (X, Y) for these two equations.
Question 2. Math Review Question:
a. [Note: Professor Kelly found physics impossible! So, be assured that you do not need to know ANY physics to answer this question-just apply the standard slope-intercept form equation to this new setting. Be brave, you non-physicists!] An experimental physicist is attempting to determine the relationship between the mass and kinetic energy of a particle in a laboratory setting. After two trials, she has observed the following data, written as an ordered pair (mass, kinetic energy): (2, 4) and (4, 10). As her lab assistant, what is the slope-intercept form of the straight line that expresses kinetic energy as a function
of mass? Based on this estimate, what kinetic energy would we expect for a particle that has a mass of 8 units? Theoretically, a particle with zero mass should have zero kinetic energy. Is our experimental model consistent with this?
b. Suppose you are given a line described by the equation y = 50 - 4x and you are told that the x value has increased by 10 units at every y value. What is the equation for the new line? Show your work.
c. Suppose you are given a line described by the equation y = 50 - 4x and you are told that the x value has doubled at every y value. What is the equation for the new line? Show your work.
d. You are given two equations.
Equation 1: y = 10 + 2x
Equation 2: y = 26 – 2x
But, you are also told that equation 1 has changed and now the y value is 10 units bigger at every x value than it was initially.
i. Write the equation that represents the new Equation1’.
ii. Given the new Equation 1’ and Equation 2, find the (x,y) solution that represents the intersection of these two lines.
Question 3. First Percentage Change Problem:
This question reviews some pretty simple math in an attempt to make your aware that you know how to change an index
number. This question allows you to practice this technique in a familiar setting so that later in the course when we do this in an economics context it might seem more familiar. Tom’s chemistry class has had three exams. The exams in the class 3 are all given the same weight in the grading scale, but each exam has a different number of total possible points. On the first exam Tom made a 60 out of 75 points, on the second exam Tom made a 51 out of a possible 60 points, and on the third exam Tom made a 40 out of 50 points.
a. What is Tom’s grade on the first exam if the first exam score was converted to a 100 point scale?
b. What is Tom’s grade on the second exam if the second exam score was converted to a 100 point scale?
c. What is Tom’s grade on the third exam if the third exam score was converted to a 100 point scale?
d. On a 100 point scale with each exam given the same weight in the calculation, what is Tom’s average grade?
e. If Tom wants to raise his average grade and the fourth exam has 60 points, how many points must Tom get on this exam?
Question 4. Second Percentage Change Problem:
Bernie stays confused about percentages and he is struggling to figure out what he needs to do on his final exam in Chemistry in order to get the B he needs. Here is the information he has: he scored a 40 out of a possible 50 points on his first midterm in the class; he scored a 15 out of 25 points on the second midterm (it was tough!) and on the third midterm he got an 85 out of a 100 points. He knows that his final will have 50 points. And, he also knows that each midterm has equivalent weight to all the other midterms and that this weight is 20% of his final grade; he also knows that the final exam will be weighted as 40% of his final grade; and to get a B in the class he knows that his total weighted average must be at least an 84 on a 100 point scale. So, what score will Bernie need to make on that final exam if he is going to get a B in the class? Show your work! Here you will find it helpful to work in decimals instead of fractions: try to do this without a calculator though!
Question 5. Opportunity Cost:
Pareto can travel from Madison to Minneapolis in one hour by taking an airplane. The same trip takes 5 hours by bus. Airfare is $90 and the bus fare is $40. If he is not travelling, Pareto can work to earn $25/hour.
Answer the following questions:
a. What is the opportunity cost if Pareto travels by bus?
b. What is the opportunity cost if Pareto travels by plane?
c. Which of these two travel options is cheaper for Pareto if Pareto considers the opportunity costs involved in this travel?
d. Suppose Walras is considering the same trip but Walras only earns $7/hour when he is not travelling. Which of these two travel options is cheaper for Walras given this information? Explain the intuition behind the difference in answers you get for Pareto and Walras.
Question 6. PPF and Opportunity Cost:
The following two graphs represent production possibility frontiers for countries A and B. Both of these countries produce milk (measured in gallons) and pork (measured in pounds).
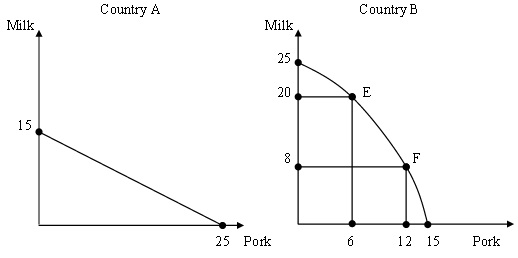
a. Explain what a production possibility frontier represents.
b. What is country A’s opportunity cost of producing one gallon of milk in terms of pork? What is country A’s opportunity cost of producing one pound of pork in terms of milk?
c. Is country B’s opportunity cost of producing one gallon of milk higher at point E than at point F? Explain.
Question 7. PPF and Comparative Advantage:
The dwarves of Erebor devote 10 hours each day to producing either beer or wine. They can produce a barrel of beer in 2 hours, but need 5 hours to make a bottle of wine. The nearby (more laid-back) elves of Mirkwood devote only 6 hours each day to working.
However, they need only 2 hours to produce either a barrel of beer or a bottle of wine.
a. Who has the comparative advantage in producing wine? Who has the comparative advantage in producing beer?
b. Draw the PPF for dwarves with wine on the x-axis. On a separate graph, do the same for the elves. What do the slopes signify?
c. The dwarves and elves trade. Draw the joint PPF for both dwarves and elves. Label the kink point on this graph. What do the slopes of this joint PPF signify?
d. What is the range of trading price for one bottle of wine in terms of barrels of beer?
e. With trade, would it be possible for each nation to consume 1 barrel of beer and 2 bottles of wine? Is the production at the efficient level? Now, (spoiler alert) the dark lord Sauron has fallen, and the men of Gondor decide to join the international trade network of theMiddle Earth. Men work 8 hours a day. They need 2 hours to produce a barrel of beer and 4 hours to produce a bottle of wine.
f. Find the joint PPF for the dwarves, the elves, and men. Label all the kink points. Draw a graph of this joint PPF and then provide the equations for each segment of the joint PPF.
g. Find the range of trading price for one barrel of beer in terms of bottles of wine.