Assignment:
1. Optical fiber has minimum transmission loss of -0.12dB/km near 1550 nm. The complex refractive index of a material is given as nc = n - jκ. What is the numerical value of κ for the optical fiber at 1550 nm, given that n ≈ 1.5.
2. (a) Calculate the reflectance (R) for normal incidence from air to Si at λ of 1μm (use n of 3.5)
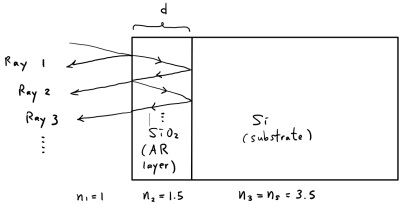
(b) An anti-reflection (AR) SiO2 layer (n of 1.5) with thickness d is coated on Si (the substrate) to reduce the optical reflection at λ of 1μm as shown below. In order to reduce reflection, rays 1, 2, 3, etc. must interfere destructively with a phase difference of π between them. Explain how this can be achieved between ray 1 and 2 if d is chosen to be quarter-λ thick (here λ refers to the wavelength in the SiO2 layer, not in free space). In your explanation, you must include all changes to the phase of the ray2 when it crosses a boundary (transmission coefficient t) and/or propagates over a distance d.
(b) The quarter-wavelength AR coating show that the reflection minimum is further achieved if the refractive index of the AR layer is √ns , where ns is the refractive index of the substrate.
3. (a) Consider an oblique incidence of light from air to glass at θ1 of 70o, calculate rs and rp for TE & TM waves respectively.
(b) When the incident wave is neither TE nor TM wave, we can express the incident wave as a superposition of TE & TM wave and each wave will be reflected accordingly to their respective reflection coefficients. Since rs and rp are different, the resultant wave from the reflected surface will undergo a change of polarization.
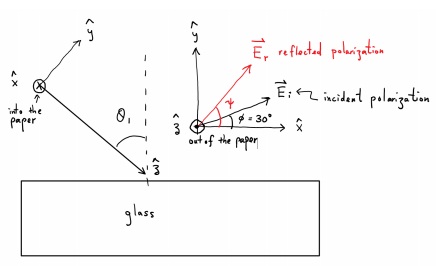
Consider an incident wave at incident angle θ1 of 700. The E field of the incident wave makes an angle ? of 30o with respect to the x as shown in the figure, calculate the angle ψ of the reflected wave.
Extra-Credit problem
4. Consider normal incident of light from air to medium 2 (n2)
(a) If n2 is lossless, shown that R + T =1 where R and T are reflectance and transmittance respectively.
(b) If n2 is lossy and is expressed as nc2 = n2 - j κ, show that R + T is also equal to 1 in accordance with conservation of power.