What is the moment of inertia of the pulley

Question

Assignment:

1. A basketball is successfully shot from an initial height of 2.0 in at an angle of 40°. The basketball passes through the hoop 10.0 m away at a height of 3.05 m.

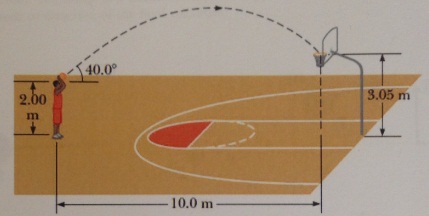
(a) Find the magnitude of the initial velocity

A. 10.67m/s

B. 10.45 m/s

C. 12.71 m/s

D. 9.66 m/s

(b) How long is the basketball in flight

A. 1.35s

B. 1.49s

C. 1.22s

D. 1.04s

(c) Find the angle with respect to the horizontal that the basketball makes when it passes through the net

A. 32.2°

B. 12.9°

C. 44.5°

D. 21.4°

2. Two masses m₂ = 6 kg and m₁ = 1 kg undergo a collision. Initially m₂ is incident with a speed v₂,0 = 5 m/s while m₁ is at rest. After the collision m₁ has a final speed v_1,f = 7.423 m/s and departs at an angle θ₁ = 30° with respect to the x axis, while m₂ has a final speed of v₂,f and departs at an angle of θ₂ with respect to the x axis. (Note: the image is a schematic and not supposed to represent the magnitude of the speeds or direction of the final velocities)

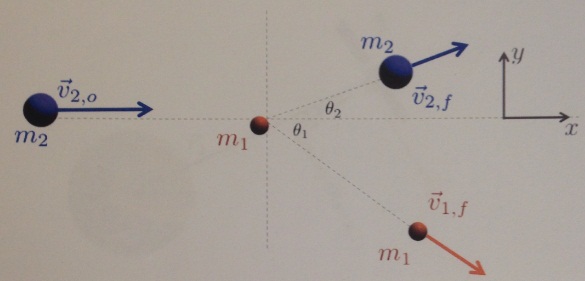
(a) Find the final speed of m₂

A. V₂, f = 3.977 m/s

B. v₂,f = 4.511 m/s

C. V₂,f = 42.26 m/s

D. v₂,f = 4.425 m/s

(b) Find the final angle of mo

A. θ₂ = 8.95°

B. θ₂ = 13.74°

C. θ₂ = 8.04°

D. θ₂ = 65.88°

(c) Find the final Kinetic Energy of the two masses combined

A. 88.6J

B. 61.6J

C. 75.0J

D. 86.3J

3. Two masses m₁ = 7kg and m₂ = 4 kg are connected via a string that runs over a massive pulley of mass M = 20 kg and radius R = 0.1 m (treat the pulley as a filled cylinder). The mass m₂ is on an incline with a coefficient of friction μk = 0.3. that is inclined at an angle of θ= 49° as shown in the diagram

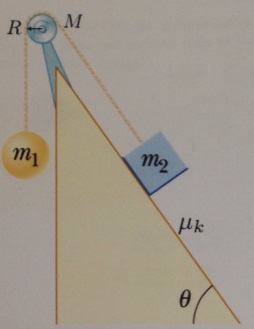
(a) What is the moment of inertia of the pulley?

A. 0.08 kg m²

B. 0.1 kg m²

C. 0.2 kg m²

D. 1 kg m²

(b) Solve the equations of motion for all three object to find the acceleration of m₁

A. -1.2 m/s²

B. 1.49 m/s²

C. 2.8 m/s²

D. 9.8 m/s²

(c) After t = 2 s what is the angular speed of the pulley assuming it starts from rest?

A. 56.4 rad/s

B. 29.8 rad/s

C. 100.8 rad/s

D. 626.0 rad/s

4. It is possible to put a satellite in a circular orbit about the Earth at a speed such that it will rotate at exactly the same rate that the earth rotates and thus stay overhead at all times. Such an orbit is called Geostationary.

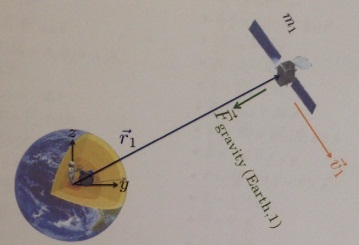
(a) Find an equation for the angular speed of a circular orbit of radius r about the earth

A. w = √G_N M_Earth/ r³

B. w = √G_N M_Earth/ r²

C. w = √G_N M_{Earth/ r}

D. w = √2G_N M_{Earth/ r}

(b) Given the Earth completes one revolution in 24 hours, what is the an- gular speed of the earth

A. 3.64 x 10^-5 rad/s

B. 7.27 x 10^-5 rad/s

C. 4.36 x 10^-3 rad/s

D. 463.2 m/s

(c) Using the result from (a) and (b) find the radius of required for a Geo¬stationary orbit. (G_N = 6.67 x 10^-11 N m² /kg² and M_Earth = 5.97 x 10²⁴ kg).

A. r = 9.34 x 10⁹ m

B. r = 2.74 x 10¹¹m

C. r = 4.22 x 10⁷ m

D. r = 8.44 x 10⁷ m