What is the minimum attainable mean-squared distortion

Question

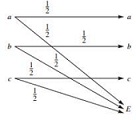
Solve the following problem:

For the channel shown in Figure .

1. Consider an extension of the channel with inputs a₁, a₂,..., a_n, outputs a₁, a₂,..., a_n, E, where P(a_i|a_i) = 1 2 , P(E|a_i) = ½, for all 1 ≤ i ≤ n, and all other transition probabilities are zero. What is the capacity of this channel? What is the capacity when n = 2m?

2. If a memory less binary equiprobable source is transmitted via the channel shown in Figure , what is the minimum attainable error probability, assuming no limit is imposed on the complexity and delay of the system? (The number of source symbols per second is equal to the number of channel symbols per second.) For what values of n in part 2 can the source be reliably transmitted over the channel?

3. If a Gaussian source distributed according to N (m, σ²) is transmitted via the channel in part 2, what is the minimum attainable mean-squared distortion in regeneration of this source as a function of n and σ²? (Again the number of source symbols per second is equal to the number of channel symbols per second, and no limit is imposed on system complexity and delay.)