Assignment:
Problem 1. You draw a coordinate system with +ˆx pointing to the right of the page and +ˆz pointing into the page. In what direction is +ˆy?
(a) into the page
(b) out of the page
(c) to the left of the page
(d) to the right of the page
(e) to the top of the page
(f) to the bottom of the page
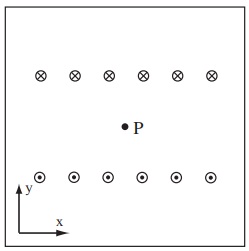
Problem 2. A positively charged particle passes through the point P in the uniform magnetic field drawn to the right. In what direction must the particle travel for the magnitude of the magnetic force to be zero?
(a) to the top of the page
(b) to the bottom of the page or to the top of the page
(c) to the left or to the right of the page
(d) into or out of the page
(e) to the left of, to the right of, into, or out of the page
(f) The magnetic force is non-zero no matter what direction the particle travels
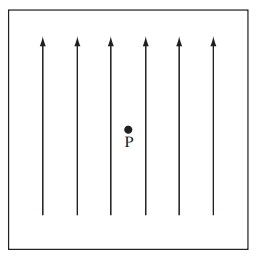
Problem 3. A pith ball, charged to 10nC, is shot into one of the Pasco lab magnets with speed 20 m s such that the velocity is perpendicular to the magnetic field. The field has a strength of 0.25T. Compute the magnitude of the magnetic force on the pith ball. This may be a very small number.
(a) 5 × 10-6N
(b) 4 × 10-4N
(c) 3 × 10-10N
(d) 3 × 10-8N
(e) 5 × 10-8N
Problem 4. An electron is accelerated to very near the speed of light (v = 3 × 108 m s ) in a particle accelerator. It travels down the center of a "beam pipe" (as shown to the right) with radius 2.5cm. What is the magnetic field (magnitude and direction, naturally) produced by the electron at the point P at the edge of the beam pipe at the same cross-section as the electron?
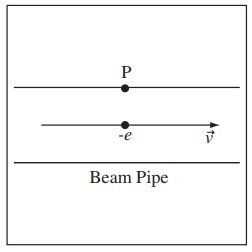
(a) B~ = 7.7 × 10-15T into the page
(b) B~ = 7.7 × 10-15T out of the page
(c) B~ = 6.5 × 10-9T into the page
(d) B~ = 6.5 × 10-9T out of the page
(e) B~ = 4.9 × 10-4T into the page
Problem 5. The figure to the right shows two parallel wires. Both carry a current I = 6A in the direction drawn. Wire 1 is fixed in place and very long. Wire 2 is 30cm long and free to move. The mass of Wire 2 is 0.7kg. The center-to-center distance between the wires is 3cm. What is the magnitude of the acceleration of Wire 2 due to the magnetic field of Wire 1?

(a) |~a| = 1.7 × 10-5m/s
(b) |~a| = 1.0 × 10-4m/s
(c) |~a| = 5.8 × 10-5m/s
(d) |~a| = 7.1 × 10-4m/s
(e) |~a| = 3.6 × 10-2m/s
Problem 6. The figure to the right shows the trajectory of a proton (mp = 1.67 × 10-27kg, qp = 1.602 × 10-19C) in a magnetic field. Suppose the field is of strength of the maximum field of a traditional superconducting magnet B = 15T. The proton travels at a speed of 1 × 107 m s , compute the radius and the direction of the orbit.
(a) 3 × 10-5m, counter-clockwise
(b) 3 × 10-5m, clockwise
(c) 2 × 10-4m, counter-clockwise
(d) 2 × 10-4m, clockwise
(e) 6 × 10-4m, counter-clockwise
(f) 6 × 10-4m, clockwise
(g) 7 × 10-3m, counter-clockwise
(h) 7 × 10-3m, clockwise
Problem 7. A long wire has a current of 6A flowing through it. What is the magnetic field produced by this wire at 30cm from the wire?
(a) 1 × 10-4T
(b) 3 × 10-5T
(c) 2 × 10-6T
(d) 4 × 10-6T
(e) 5 × 10-5T
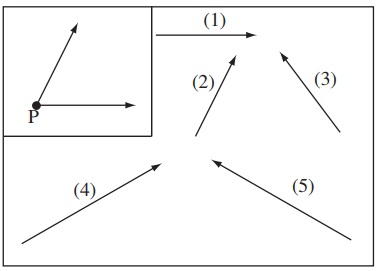
Problem 8. The figure below shows the magnetic forces exerted on a charged particle placed at point P. Select the vector that correctly represents the total force on the particle at P.
(a) Vector
(b) Vector
(c) Vector
(d) Vector
(e) Vector
Problem 9. An infinite solenoid has 15 turns per meter and a current of 8.0A. What is the magnetic field INSIDE the solenoid?
(a) 1.5 × 10-4T
(b) 1.5 × 10-5T
(c) 3 × 10-2T
(d) 0
(e) This cannot be determined because the distance from the solenoid's axis is not given.
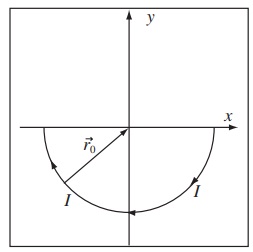
Problem 10. A half loop of wire centered at the origin occupies the -y portion of the x - y plane. A current I flows clockwise when viewed from the +z side of the plane. The radius of the half loop is 5cm and the loop carries a current of 3A. Compute the magnetic field at the origin.
(a) 0
(b) -1.2 × 10-5Tˆz
(c) +1.2 × 10-5Tˆz
(d) +1.9 × 10-5Tˆz
(e) -1.9 × 10-5Tˆz
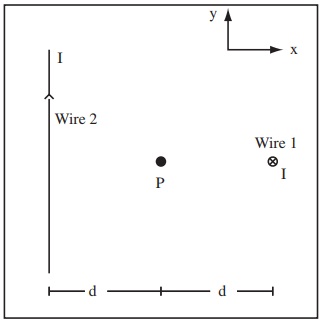
Problem 11. Two infinite straight wires carry current I = 2A as shown to the right. One wire is parallel to the y axis and one wire is parallel to the z axis. The current directions are as drawn. The distance from each wire to point P is 3cm. Calculate the magnetic field at point P. Be sure to report the magnetic field as a vector.
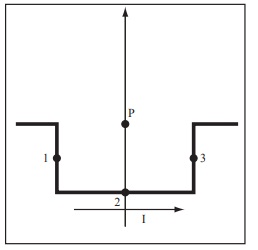
Problem 12. The figure to the right shows a piece of wire which carries a current of 3A. The vertical segments 1 and 3 are 5cm long and the segment 2 is 10cmlong.
(a) Compute the magnetic field, B~ 1P , of segment 1 at the point P approximating the segment as a finite current element.
(b) Compute the magnetic field, B~ 2P , of segment 2 at the point P approximating the segment as a finite current element.
(c) Compute the magnetic field, B~ 3P , of segment 3 at the point P approximating the segment as a finite current element.
(d) Compute the total magnetic field at point
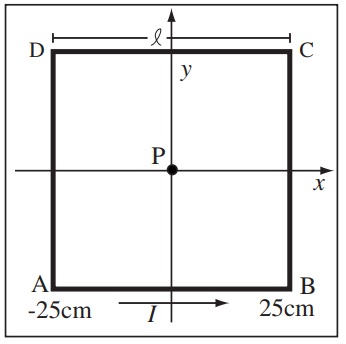
Problem 13. The figure below shows a square coil of wire with sides of length l = 50cm.
The coil has a single turn and carries a current I = 6A. This problem asks you to compute the field at the point P at the center of the coil in two different ways. You may exploit symmetry to simplify the problem if you wish.
(a) Compute the magnetic field at point P approximating the field of each side of the square as a single current element using the finite current element approximation. Report both a symbolic and numeric expression for the field. Carefully show all steps of your calculation.
(b) Calculate the exact magnetic field at P starting from the Biot-Savart Law. Report both a symbolic and numeric expression for the field. Note, the field calculated in Part (a) may not be a good approximation to the exact field in Part (b)
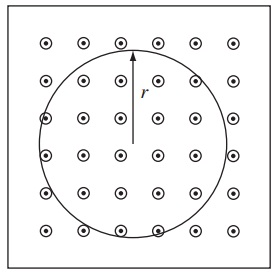
Problem 14. The figure to the right shows a cross-section of a solenoid. The current in the solenoid flows into the page at the top of the solenoid and out of the page at the bottom. The solenoid has radius R = 10cm and is wound with 200 turns over a distance of 30cm. Treat the solenoid using the infinite solenoid approximation.
(a) What is the direction of the magnetic field of the solenoid at the point P?
(b) You would like to use the solenoid to lift a conducting rod running through the point P as part of an electromagnetic latch. In what direction must current flow through a rod running through P to produce a force in the +ˆy direction?
(c) If the length of the rod running through P is the same as the radius of the solenoid and the mass of the rod is 0.07kg and if both the solenoid and the rod carry the same current, how much current is required to balance the downward force of gravity on the rod thus floating the rod? Gravity acts toward the bottom of the page.