Part -1:
Problem 1
The Chief Information Officer (CIO) at Old Dominion University -ODU- is trying to improve the university's information network security. The CIO is trying to evaluate a new intrusion detection technology in the market for possible replacement for the existing system. An intrusion detection system sounds an "alarm" each time possible malicious attack on a network is detected. The following information is provided:
n Probability of an actual malicious attack is 0.01.
• For the currently installed system, the probability of an alarm given that there is an actual malicious attack is 0.9, while the probability of an alarm given there is not a malicious attack is 0.25.
• For the new technology, the probability of an alarm given that there is an actual malicious attack is 0.8, while the probability of an alarm given there is not a malicious attack is 0.1.
n The CIO assumes that there are only two types of events: either there is or there is no malicious attack.
• The CIO is using "evidence ratio," described as P(B IA) / P(B I A') as a way to compare the technologies. Please help the CIO compare the new technology with the currently installed system by answering the following questions:
1. Based on the definition of evidence ratio in the previous paragraph, what is the evidence ratio for the currently installed system?
2. What is the evidence ratio for the new technology?
3. Which technology is better? Existing technology or new technology?
Problem 2
Frodo, a junior engineer at Baggins Metal Works is considering the introduction of a new line of products. in order to produce the new line, the company needs either a major or minor renovation of the current plant. The market for the new line of products could be either favorable or unfavorable, each with equal chance of occurrence. The company has the option of not developing the new product line at all.
With major renovation, the company's payoff from a favorable market is $100,000, from an unfavorable market, $ -90,000. Minor renovation and favorable market has a payoff of $40,000 and an unfavorable market, 5-20,000. Not developing the new product line effectively has $0 payoff.
Frodo realizes that he should get more information before making his final decision. He contracted with Gandalf Market Research to conduct a market analysis to determine for certain if the market will be favorable or unfavorable. How much is the maximum amount Frodo should be willing to pay for this accurate information? (Please indicate your answer to the nearest whole number)
Part -2:
Problem 1
There are two sub-systems (1 and 2). Failure of sub-systeml will make sub-system2 35% inoperable, while failure of sub-system2 will make sub-systeml 50% inoperable
1. Matrix A can be written as:
Suppose that sub-system2 is attacked with intensity h = 90%. Using matrix equation x = Ax + c, where x is the inoperability of the sub-systems, A is the dependency matrix, and c is the intensity of attack, please match the values to the following questions
2. What is the resulting value of x1?
3. What is the resulting value of x2?
Problem 2
Apply Gorda algorithm to score and rank the risk events shown.
|
Criteria
|
1.1 Telephone
|
1.2 Cellular
|
2. Cable
|
|
Undetectabilitv
|
High
|
Low
|
High
|
|
Uncontrollability
|
High
|
Med
|
High
|
|
Multiple Paths to Failure
|
High
|
Med
|
High
|
|
Irreversibility
|
High
|
High
|
Low
|
|
Duration of Effects
|
High
|
High
|
High
|
|
Cascading Effects
|
Low
|
High
|
High
|
|
Operating Environment
|
High
|
Med
|
High
|
|
Wear and Tear
|
High
|
Med
|
High
|
|
Hardware' Sof tw are/Human/Organizational
|
High
|
High
|
High
|
|
Complexity and Emergent Behaviors
|
High
|
High
|
High
|
|
Design Immaturity
|
High
|
High
|
Med
|
1. What is the score of "Telephone"?
2. What is the score of "Cellular"?
3. What is the score of "Cable"?
Problem 3
John Doe is a rational person whose satisfaction or preference for various amounts of money can be expressed as a function U(x) = (x/100)^2, where x is in $.
1. How much satisfaction does $20 bring to John?
If we limit the range of U(x) between 0 and 1.0, then we can use this function to represent John's utility (i.e. U(x) becomes his utility function).
2. What is the shape of his utility function?
CI Concave
m Convex
m Straight line
q None of these
3. What does this graph show about John's incremental satisfaction?
q Increases with increasing x
q Decreases with increasing x
q Does not change with k
m None of these
4. "The shape of John's utility function shows that he is willing to accept more risk than a risk-neutral person."
True
False
5. John is considering a lottery which payoff $80 forty percent of the time, and $10 sixty percent of the time. If John plays this lottery repeatedly, how much will be his long-term average satisfaction?
6. For John, what certain amount would give him satisfaction equal to this lottery? Express your answer to nearest whole $.
Part -3:
1. The Weibull hazard rate function λ(t) is given by:
λ(t) = (β/θ)t
Where β is the shape parameter and θ is the scale parameter. Obtain an expression for a reliability function.
2. Assume load and capacity are exponentially and normally distributed, respectively. The mean load is equal to 14000psi and the values of the mean and standard deviation associated with the normal distribution are 21000 and 3000 psi respectively. Calculate the reliability.
3. Problem 8-12 from textbook:
The following numbers of bends to failure were recorded for 20 paper clips:
11,29,15,20,19,11,12,9,9,8,13,20,11,22,20,9,25,19,11 and 10.
A. Make a nonparametric plot of R(t), the reliability.
B. Attempt to fit your data to Weibull and Normal Distributions then determine the parameters.
C. Briefly discuss your results.
4. Problem 6-8 from textbook:
A device has a constant failure rate of 0.7/year.
A. What is the probability that the device will fail during the second year of operation.
B. If upon failure the device is immediately replaced, what is the probability that there will be more than one failure in 3 years operation?
5. Problem 12-7 from textbook
There exists a nuclear reactor plant with a system to deliver emergency cooling with 2 pumps and 4 valves. In the event of an accident the protection system delivers an actuation signal to the two identical pumps and the 4 identical valves. The pumps start up, the valves open and the liquid coolant is delivered to the reactor. The following failure probabilities are found to be significant:
P(ps)=10-5, the probability that the protection system will not deliver a signal to the pump and the valve actuators.
P(p)= 2 x 10-2, the probability that a pump will fail to start when the actuation signal is received.
P(v)= 10-1, the probability that a valve will fail to open when the actuation signal is received.
P(r) =0.5 x 10-5, the probability that the reservoir will be empty at the time of the accident.
A) Draw a fault tree for the failure of the system to deliver any coolant to the primary system in the event of an accident.
B) Evaluate the probability that such a failure will take place in the event of an accident.
1. There is a contractual requirement to demonstrate with 90% confidence that a vehicle can achieve a 100-km mission with a reliability of 99%. The acceptance test is performed by running 10 vehicles over a 50,000-km test track.
(a). What is the contractual MTTF? Assuming an exponential distribution:
(b). What is the maximum number of failures that can be experienced on the demonstration test without violating the contractual requirement? (Note: Assume an exponential distribution.)
2. The failure rate for a high-speed fan is given by Mt) = (2 x 104 + 3 x 10-60 / hr, Where t is in hours of operation. The required design-life reliability is 0.95.
(a) How many hours of operation should the design life be?
(b) If, by preventive maintenance, the wear contribution to the failure rate can be eliminated, to how many hours can the design life be extended?
(c) By placing the fan in a controlled environment, we can reduce the contribution of random failure to Mt) by a factor of two. Then, without preventive maintenance, to how many hours may the design life be extended?
(d) What is the extended design life with both preventive maintenance and controlled environment?
3. The following table gives a series of times to repair (man-hours) obtained for a diesel engine.
|
11.6
|
7.9
|
27.7
|
17.8
|
8.9
|
22.5
|
|
3.3
|
33.3
|
75.3
|
9.4
|
28.5
|
5.4
|
|
10.3
|
1.1
|
7.8
|
41.9
|
13.3
|
5.3
|
(a) Estimate the MTTR.
(b) Estimate the repair rate and its 90% confidence interval assuming that the data is exponentially distributed.
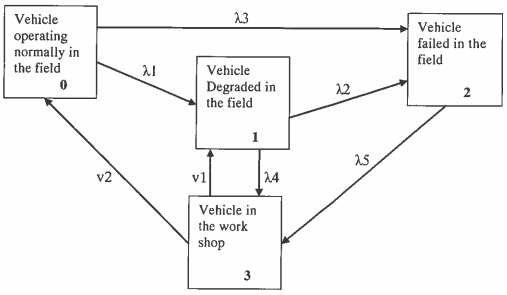
4. Set up the associated Markov differential equations for the following system.
λ3= Failure rate from State-0 to State-2
λ4= Failure rate from State-I to State-3
λ5= Failure rate from State-2 to State-3
v1= Repair rate from State-3 to State-I
v2= Repair rate from State-3 to State-0
Attachment:- 1.pdf