Question 1. Jar Jar Binks is a resident of the Gungan kingdom. He earns $1000 per year working as a senator, and he spends this income on coconuts (C) and fish (F). The price ofcoconut s is $25 and the price of fish is $10. Suppose that Jar Jar values coconuts and fish equally. His utility function is given by the following equation where U is the amount of utility: U = 2C + 2F
a) Given the information, what is the equation for Jar Jar’s budget line? Assume that Jar Jar spends all of his income on coconuts and/or fish. Graph this budget line with coconuts on the x - axis and fish on the y - axis. Label this budget line BL1.
b) Given the above information, draw at least four of Jar Jar's indifference curves in a graph that also contains BL1. Given the budget BL1, how many coconuts and fish will Jar Jar Binks choose to consume ? What is his utility level given this consumption bundle ?
c) Now, suppose that Jar Jar’s income doubles. At the same time, t he price of coconuts drops to $20, while the price for fish rises to $20. Find the new budget line for Jar Jar and graph it in a new graph where coconuts are measured on the x - axis and fish are measured on the y - axis. Label this budget line BL2. Write the equation fo r BL2.
d) Given budget BL2, how many coconuts and fish does Jar Jar eat? What is his utility level? Illustrate his optimal consumption bundle(s) with a graph. (Hint: think about this one very carefully!)
e) Go back to the original situation (income of $1000, price of $25 and $10 for coconu ts and fish , respectively). Now, the Gungan king dictates that nobody c an eat more than 50 fish per year, to protect the local fish species. Graph the new budget line for Jar Jar. Label it BL3.
f) Under the budget BL3, how many coconuts and fish would Jar Jar Binks eat? What is his utility level?
g) Compare you answers in b) and f). Is Jar Jar Binks better off from the new restriction on fish consumption, or is he worse off? Briefly explain why.
Question 2. A poor graduate student at UW Madison survives on cheap pizzas (x) and Badger Market coffee (y). His utility from consuming these two goods is given by: U = x2y2 His marginal utility from eating one slice of pizza is 2xy2, and his marginal utility from drinking one cup of coffee is 2x2y .
a) The current price for one slice of pizza is $3, and the price for one cup of coffee is $1. The graduate student can spend $600 on these two goods. Give n this information, provide an equation relating the graduate student's consumption of x and y if he is maximizing his utility. This equation is called an “optimality condition”.
b) When the graduate student is behaving optimally, many slices of pizza and cups of coffee does he choose to purchase? What is his utility level? In a graph draw the graduate student ' s budget line and an indifference curve showing his utility maximizing choice. Put pizza (x) on the horizontal axis. Label the optimal bundle of pizza and coffee as point A.
c) Badger Market decides to raise the price of one cup of coffee to $2. How many pizza and coffee does the graduate student now purchase, if he is maximizing his utility? How much is he worse off? Draw the new budget line and the indifference curves. Label the new o ptimal bundle as point B.
d) We now want to compute the income and substitution effects of the price change in part (c). To do this we must compute the point “C” that lies on an “imaginary” budget line. There are two features of point C: (i) it gives the same utility as the bundle chosen under the original prices, so it lies on the same indifference curve as point A; (ii) the imaginary budget line has the same slope as the second budget line, so the slope of the indifference curve at point C is equal to the slope of budget line 2. Importantly that means that the imaginary budget line does not pass through point A! Indeed, we do not know the income of the imaginary budget line, tho ugh we do know its slope. This information about slope gives you an optimality condition and the second equation you need is that the utility from the bundle at C is the same as the utility from the bundle at A. Use these two equations to find point C and illustrate on a diagram. Once you find the coordinates of bundle C, calculate the income of this imaginary budget line. Hint: the numbers here will get messy - use a calculator and carry all numbers out to two places past the decimal.
e) Use point C to calculate the income and substitution effects of the increase in coffee price (in terms of the change in the quantity of coffee consumed). Hint: in this problem you will calculate the income and substitution effects along the y - axis and, if you can do this, you should be ready to do the simpler examples where the income and substitution effects are calculated along the x - axis.
f) Due to the loud protests from impoverished graduate students, the university decides to raise their stipend (salary). How much should the stipend raise be, such that ou r graduate student could return to his original utility level before the price increase? (In other words, by how much would his stipend have to change to be able to afford the bundle at point C?)
3. The Silph Company employs workers to make scopes. The following table shows the short-run relationship for the company between workers employed and scopes produced . You are told that t he wage for each worker is $10 and that the raw material to make a single scope costs $20.
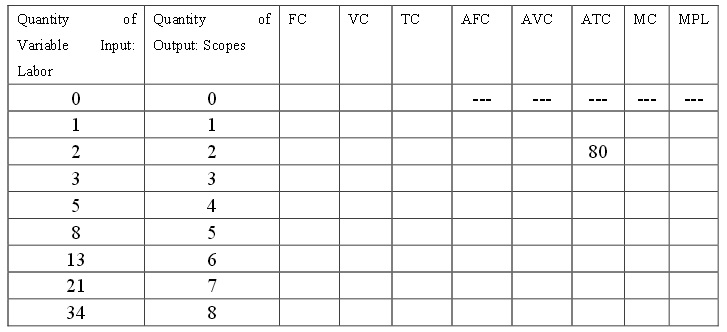
a) Fill out the table above using the given information.
b) Does Silph Co. experience diminishing returns to labor? Use the last column of the table to answer this question.
c) Assume that Silph Co. is in a perfectly competitive market for scopes, and the current market price for one scope is $60. How many scopes should Silph Co. produce? How many workers does it hire? Does the company make a profit?
d) In the long run, what is the minimum price for one scope such that the company could stay open?
Question 4. Consider the taco stands on State Street. Suppose that the taco market on State Street is a perfect competitive market, where all taco stands are exactly the same (i.e. producing the exact same tacos and having the exact same cost features). The market demand for tacos is given by the demand curve where P is the price per taco and Q is the market quantit y of tacos:
P = 100 – 2Q
Each taco stand faces a marginal cost curve given by the following equation where q is the quantity of tacos produced by the firm:
MC = 4q
and a total cost curve given by:
TC = 2q2 + 8
a) For each taco stand, what is the fixed cost (FC)? What is the average fixed cost (AFC) curve and the average total cost (ATC) curve?
b) What is the break - even price for each taco stand?
c) What is the shut - down price? ( For simplicity, assume that q does not need to be an integer)
d) Assume that the current price for one taco on State Street is $10. How many tacos does each taco stand produce? Suppose that there is no cost in setting up/closing down a taco stand. Will we witness entry of new taco stands int o the market, or exit of existing stands from the market?
e) Imagine that you are one of the taco stand owners. The current price for one taco has dropped from $10 to $7. Describe what you would do in the short run and in the long run.
f) In the long run, what would the price for one taco be on State Street? How many taco stands will stay in the market?
Question 5. Observe the following cost graph of a manufacturing firm:
a) Is the firm in a perfectly competitive market? Explain your reasoning.
b) Find the average fixed cost (AFC) curve.
c) Find the marginal cost (MC) curve.
d) If the firm chooses to maximize its profit, at what quantity should it produce? Label the areas in the graph representing revenue, total fixed cost and total variable cost when the firm chooses the optimal quantity. Assume the firm can only charge one price for the good.