What is the coefficient of restitution for the collision

Question

Assignment:

1. A wooden plank is placed horizontally on the floor. A wedge of wood (object A, m_A = 10kg), cut with an angle of p = 20°, is placed on top of the plank. A block of wood (object B, m_B = 20kg) is placed on top of the wedge. Both objects and the plank are initially at rest, and the coefficients of static friction between the surfaces are p_s,_AB = 0.7 and u_s,_pA = 0.3, respectively. One end of the plank is very slowly raised up off the floor (0 starts at 0° and increases slowly from there).

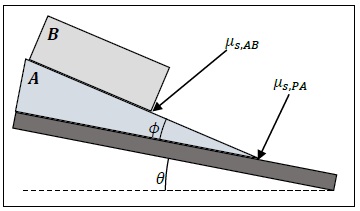
a. Assuming that object B doesn't slide on object A, at what angle (0) will the combined object AB begin to slide?

b. Assuming that object A doesn't slide on the plank while object B is free to slide, at what angle (0) will object B begin to slide?

c. From the formulas used to calculate parts (a) and (b), derive a formula defining the necessary relationship between the values of u_s,AB and u_s,_PA such that both A and B would begin to slide at the same angle (0)?

2. Block 1 is placed on a 30° incline, and is attached to block 2 by a rope. Block 2 is hanging from a pulley over the top edge of the incline and is also completely submerged in a tank of water.

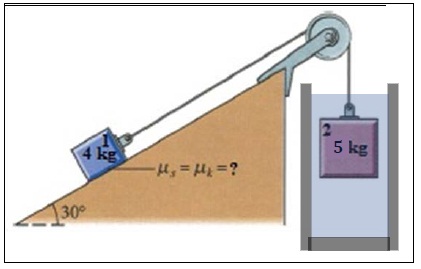
a. For what block 2 density could static equilibrium be maintained without static friction?

b. If block 2 were aluminum, what is the smallest coefficient of static friction required to for static equilibrium?

c. If the coefficient of static friction were u_s = 0.30, for what maximum and minimum block 2 densities could static equilibrium be maintained?

3. Given the vector relationship and vector definitions below, find the magnitude and direction of E¯.

A¯ - B¯ + 1/2 c¯ + 1/3 (E¯- D¯) = 0

A¯ = 21 + 59

B¯ = (7, -4)

C¯= 9 at 210°

D¯= 12 at 25° above -x

4. A 480 kg car moving at 16.2 m/s hits, from behind, another car of mass 570 kg moving at 13.3 m/s in the same direction. The second car's new velocity is 15.1 m/s.

a. What is the coefficient of restitution for the collision?

b. What percentage of the kinetic energy is lost in the collision?

c. With what speeds would the cars rebound if the collision was perfectly elastic?