What is the best power allocation strategy by transmitter

Question

Solve the following problem:

A binary communication system uses antipodal signals s₁(t) = s(t) and s₂(t) = -s(t) for transmission of two equiprobable messages m₁ and m₂. The block diagram of the communication system is given in Figure .

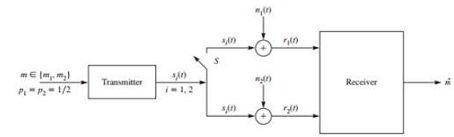
Message s_i(t) is transmitted through two paths to a single receiver, and the receiver makes its decision based on the observation of both received signals r₁(t) and r₂(t). However, the upper channel is connected by a switch S which can either be closed or open. When the switch is open, r₁(t) = n₁(t); i.e., the first channel provides only noise to the receiver. The switch is open or closed randomly with equal probability, but during the transmission it will not change position. Throughout this problem, it is assumed that the two noise processes are stationary, zero-mean, independent, white and Gaussian processes each with a power spectral density of N₀/2.

1. If the receiver does not know the position of the switch, determine the optimal decision rule.

2. Now assume that the receiver knows the position of the switch (the switch is still equally likely to be open or closed). What is the optimal decision rule in this case, and what is the resulting error probability?

3. In this part assume that both the transmitter and the receiver know the position of the switch (which is still equally likely to be open or closed). Assume that in this case the transmitter has a certain level of energy that it can transmit. To be more specific, assume that in the upper arm αsi(t) and in the lower arm β_si(t) is transmitted, where α, β ≥ 0 and α₂ + β₂ =

4. What is the best power allocation strategy by the transmitter (i.e., what is the best choice for α and β), what is the optimal decision rule at the receiver, and what is the resulting error probability?