Weekly Problems #2:
1. The following gives the number of pints of type A blood used at Woodlawn Hospital in the past 6 weeks:
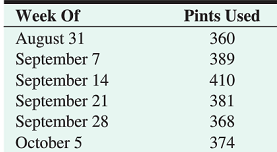
a) Forecast the demand for the week of October 12 using a 3-week moving average.
b) Use a 3-week weighted moving average, with weights of .1, .3, and .6, using .6 for the most recent week. Forecast demand for the week of October 12.
c) Compute the forecast for the week of October 12 using exponential smoothing with a forecast for August 31 of 360 and α= .2.
2. Income at the law firm Smith and Jones for the period February to July was as follows:

Use trend-adjusted exponential smoothing to forecast the law firm's August income. Assume that the initial forecast for February is $65 000 and the initial trend adjustment is 0. The smoothing constants selected are α=.1 and β=.2.
3. Page Engineering designs and constructs air conditioning and heating systems for hospitals and clinics. Currently, the company's staff is overloaded with design work. There is a major design project due in 8 weeks. The penalty for completing the design late is $14 000 per week, since any delay will cause the facility to open later than anticipated, and cost the client significant revenue. If the company uses its inside engineers to complete the design, it will have to pay them overtime for all work. Page has estimated that it will cost $12 000 per week (wages and overhead), including late weeks, to have company engineers complete the design. Page is also considering having an outside engineering firm do the design. A bid of $92 000 has been received for the completed design. Yet another option for completing the design is to conduct a joint design by having a third engineering company complete all electromechanical components of the design at a cost of $56 000. Page would then complete the rest of the design and control systems at an estimated cost of $30 000.
Page has estimated the following probabilities of completing the project within various time frames when using each of the three options. Those estimates are shown in the following table:
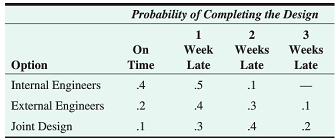
What is the best decision based on an expected monetary value criterion? (Note: You want the lowest EMV because we are dealing with costs in this problem.)
4. McBurger, Inc. wants to redesign its kitchens to improve productivity and quality. Three designs, called designs K1, K2, and K3, are under consideration. No matter which design is used, daily demand for sandwiches at a typical McBurger restaurant is for 500 sandwiches.
A sandwich costs $1.30 to produce. Non-defective sandwiches sell, on the average, for $2.50 per sandwich. Defective sandwiches cannot be sold and are scrapped.
The goal is to choose a design that maximizes the expected profit at a typical restaurant over a 300-day period. Designs K1, K2, and K3 cost $100 000, $130 000, and $180 000 respectively. Under design K1, there is a .80 chance that 90 out of each 100 sandwiches are non-defective and a .20 chance that 70 out of each 100 sandwiches are non-defective. Under design K2, there is a .85 chance that 90 out of each 100 sandwiches are non-defective and a .15 chance that 75 out of each 100 sandwiches are non-defective. Under design K3, there is a .90 chance that 95 out of each 100 sandwiches are non-defective and a .10 chance that 80 out of each 100 sandwiches are non-defective. What is the expected profit level of the design that achieves the maximum expected 300-day profit level?