Assignment:
Question 1. Military specifications often call for electronic devices to be able to withstand accelerations of 10 g. To make sure that their products meet this specification, manufacturers test them using a shaking table that can vibrate a device at various specified frequencies and amplitudes.
The acceleration of gravity is 9.81 m/s 2.
If a device is given a vibration of amplitude 9.9 cm, what should be its frequency in order to test for compliance with the 10 g military specification?
Question 2. When a mass of 28 g is attached to a certain spring, it makes 18 complete vibrations in 3.6 s.
What is the spring constant of the spring?
Question 3. Given: G = 6.67259 × 10-11 N m2 /kg2 An object of mass 144 kg moves in a smooth straight tunnel dug through the center of a planet of mass 8.78×1024 kg and radius 2.21× 106 m as shown in the figure.
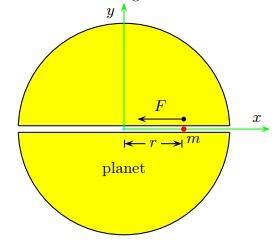
Determine the effective force constant k of the harmonic motion; i.e., use Hook's Law F = -k x .
Question 4. Find the maximum speed of the object.
Question 5. An m = 4.8 kg lead ball is hanging from a k = 559 N/m spring. The ball is pulled 23 cm below the equilibrium position and released
with zero initial velocity.
What is the speed of the ball 2.09 s after it was released? (Mind the units.)
Question 6. A solid cylinder of mass M = 5.7 kg and radius R = 6.7 cm is yoked to a spring as shown in the figure below:
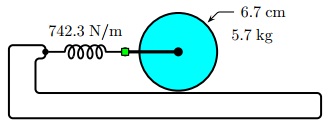
To be precise, the axle of the cylinder is attached to a horizontal spring of force constant k = 742.3 N/m. The cylinder rolls back-andforth on a horizontal base without slipping. For simplicity, assume that the spring, the axle and the yoke which connects them have negligible masses compared to the cylinder itself.
What is the angular frequency of the cylinder rolling back-and-forth around the equlibrium position?
Question 7. A large block with mass 26 kg executes horizontal simple harmonic motion as it slides across a frictionless surface with a frequency 2.17 Hz . Block smaller block with mass 8 kg rests on it, as shown in the figure, and the coefficient of static friction between the two is µs = 0.609 .
The acceleration of gravity is 9.8 m/s2
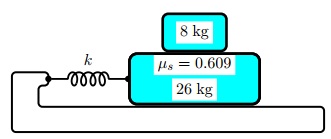
What maximum amplitude of oscillation can the system have if the block is not to slip?
Question 8. A uniform plank of mass M = 7.9 kg and length L = 32 cm is pivoted at one end. A vertical spring of force constant k = 420 N/m
is attached to the plank at a distance l = 21 cm from the pivot end, as shown in the figure below:
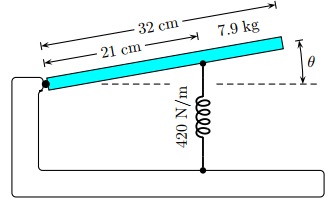
The height of the pivot has been adjusted so that the plank will be in equilibrium in the horizontal position θ = 0.
Find the period of small oscillation of the plank about the equilibrium point.
Question 9. Given: Icm = 2 5 m r2 for a solid sphere.
A solid sphere has mass 5 kg , radius 4 cm . The sphere rolls without slipping in a spherical bowl of radius 32 cm .
The acceleration of gravity is 9.8 m/s2.
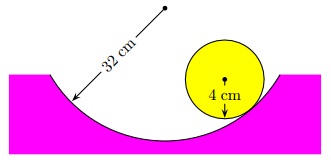
Determine (for small displacements from equilibrium) the period of harmonic oscillation which the sphere undergoes.
Question 10. A visitor to a lighthouse wishes to determine the height of the tower. The visitor ties a spool of thread to a small rock to make a simple pendulum, then hangs the pendulum down a spiral staircase in the center of the tower. The period of oscillation is 9.42 s.
The acceleration of gravity is 9.81 m/s 2 .
What is the height of the tower?
Question 11. A uniform disk of radius 4.1 m and mass 3.7 kg is suspended from a pivot 1.189 m above its center of mass.
The acceleration of gravity is 9.8 m/s2
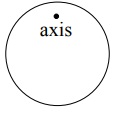
Find the angular frequency ω for small oscillations.
Question 12. Consider a mass M = 4.9 kg hanging from a spring with force constant k = 6900 N/m. Let x denote the vertical coordinate of the mass; the mass is inequilibrium at x = 0; positive direction is up.
At time t0 = 0 the mass is moved to x0 = +5 cm and given initial speed v0 = -1.4 m/s. (Mind the units!) Subsequently, it oscillates according to x(t) = A × sin(ωt + ?0).
What is the amplitude A of this oscillation?
Question 13. What is the initial phase ?0? Give an answer between -π and +π.
Question 14. What is the total energy of the oscillation?
Question 15. When is the kinetic energy of the oscillator is equal to twice the potential energy - K = 2U - for the first time (after T0 = 0)?
Question 16. A steel piano wire 1.47 m long has a crosssectional area of 0.00459 cm2 . The Young's modulus for the wire is 2 × 1011 N/m2 . When under a tension of 89.6 N , how much does it stretch?
Question 17. A solid metal sphere of volume 1.24 m3 is lowered to a depth in the ocean where the water pressure is equal to 1.3 × 107 N/m2 .
The bulk modulus of the metal from which the sphere is made is 9.69 × 109 N/m2 .
Given: The atmospheric pressure is 101300 Pa.
What is the change in the volume of the sphere?
Question 18. The distortion of the Earth's crystal plates is an example of shear on a large scale. A particular crystal rock has a shear modulus of 1.8 × 1010 Pa.
What shear stress is involved when a 9 km layer of this rock is sheared through a distance of 4.6 m?