Discuss the below:
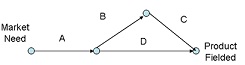
Q1. You are in charge of a major new product development project for your company. Instead of presenting the details of your analysis, you aggregate all three elements of this product into a simple PERT network to present to senior management as shown below. You would like to introduce simulation as a project management tool for your company and you feel that this product has enough visibility to persuade senior management of its utility. Using Crystal Ball, develop a plot of project duration as a function of probability of completion
Where
A = Requirements gathering (uniformly distributed varying between 3 and 5 week)
B = Develop prototype and test market (normally distributed with a mean of 5 weeks and a standard deviation of 3)
C = Manufacture and distribute new product (uniformly distributed varying between 5 and 8 week)
D = Advertising, trade shows, market to distributors, etc. (fixed at 11 weeks)
Q2. As a new manager of manufacturing of specialty devices for Farr Pharmaceutical Devices, you need to improve turnaround time. You currently are operating one manufacturing line. You did a queuing analysis on the operation, but found the mathematical solution did not accurately model the real world system; therefore, you decide to manually simulate the operation. You analyzed last year's data and arrived at the following distribution of arrival intervals and service times:
Distribution of Arrival Intervals
|
Arrival Interval (days)
|
Number of
Occurrences
|
Probability P(x)
|
Cumulative Probability
|
Random Number Range
|
|
1.0
|
4
|
|
|
|
|
2.0
|
6
|
|
|
|
|
3.0
|
3
|
|
|
|
|
4.0
|
7
|
|
|
|
Manufacturing times are uniformly distributed and vary between 1 and 3 days.
x=a+r(b-a)= 1+2r
Use the table below to manually simulate (hint - do NOT round your numbers to integer values) the process of your specialty manufacturing operation.
|
Job #
|
r1
|
Inter-arrival time
|
Total Clock Time
|
Start Manu Time
|
Wait Time
|
Queue Length After Entry
|
r2
|
Manu Time
|
Depart Clock
|
Time in System
|
|
1
|
---
|
---
|
0
|
0.00
|
0.00
|
0
|
0.93
|
|
|
|
|
2
|
0.06
|
|
|
|
|
|
0.72
|
|
|
|
|
3
|
0.47
|
|
|
|
|
|
0.83
|
|
|
|
|
4
|
0.3
|
|
|
|
|
|
0.35
|
|
|
|
|
5
|
0.97
|
|
|
|
|
|
0.17
|
|
|
|
|
6
|
0.96
|
|
|
|
|
|
0.82
|
|
|
|
|
7
|
0.22
|
|
|
|
|
|
0.63
|
|
|
|
|
8
|
0.16
|
|
|
|
|
|
0.68
|
|
|
|
|
9
|
0.52
|
|
|
|
|
|
0.95
|
|
|
|
|
10
|
0.98
|
|
|
|
|
|
0.07
|
|
|
|
Determine the average waiting time, average queue length, and average time in the system.