1. Show that
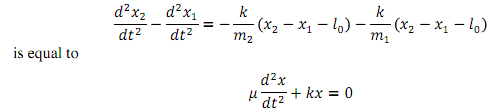
using the definitions for the relative coordinate and reduced mass.
2. A coordinate transformation is performed to express the harmonic oscillator problem involving two masses coupled by a spring in terms of the motion of the system's center of mass and the motion of the system's reduced mass.
a. Calculate the reduced mass of the following pairs of atoms:
i. C and O
ii. C and H
b. What general conclusions can you reach about the relationship between the relative sizes of the two masses and the corresponding reduced mass?
c. Locate the position of the center of mass for the pairs of atoms given below. Place the carbon atom at the origin of the coordinate system.
i. C and O. A typical C-O bond length is 1.43Å
ii. C and H. A typical C-H bond length is 1.10Å.
d. What can you conclude about the position of the center of mass when the two masses are nearly equal in contrast with the situation where there is a significant difference between the masses?
3. Show whether the following functions are even, odd, or neither:
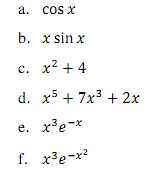
Attachment:- Homework.rar