Problem:
Tom's, Inc., produces various Mexican food products and sells them to Western Foods, a chain of grocery stores located in Texas and New Mexico. Tom's, Inc., makes two salsa products: Western Foods Salsa and Mexico City Salsa. Essentially, the two products have different blends of whole tomatoes, tomato sauce, and tomato paste. The Western Foods Salsa is a blend of 50% whole tomatoes, 30% tomato sauce, and 20% tomato paste. The Mexico City Salsa, which has a thicker and chunkier consistency, consists of 70% whole tomatoes, 10% tomato sauce, and 20% tomato paste. Each jar of salsa produced weighs 10 ounces. For the current production period, Tom's, Inc., can purchase up to 280 pounds of whole tomatoes, 130 pounds of tomato sauce, and 100 pounds of tomato paste; the price per pound for these ingredients is $0.96, $0.64, and $0.56, respectively. The cost of the spices and the other ingredients is approximately $0.10 per jar. Tom's, Inc., buys empty glass jars for $0.02 each, and labeling and filling costs are estimated to be $0.03 for each jar of salsa produced. Tom's contract with Western Foods results in sales revenue of $1.64 for each jar of Western Foods Salsa and $1.93 for each jar of Mexico City Salsa.
Letting W= jars of Western Foods Salsa M=jars of Mexico City Salsa
The sensitivity report is shown in figure below.
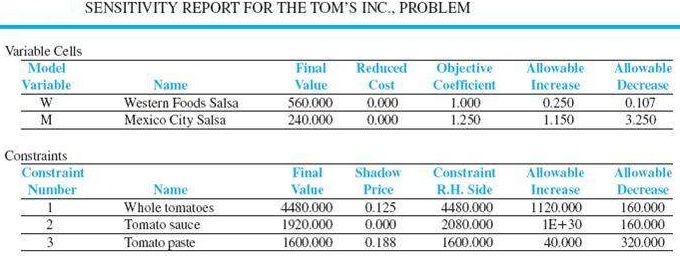
a) What is the optimal solution, and what are the optimal production quantities? W=1.0 M=1.250 PROFIT=800000
b) Specify the objective coefficient ranges.
VARIABLE lower limit upper limit
Western Foods .107 .250
Mexico City 3.250 1.150
What are the shadow prices for each constraint?
Constraint Shadow Price
Whole tomatoes .125
Tomato Sauce 0.00
Tomato Paste 1.88
Interpret each shadow price.The shadow price is the cost for each additional unit
Identify each of the right-hand-side ranges.Constraint Rthand side range
Constraints lower limits
Whole tomatoes 1120.0 160.0
Tomato Sauce 0.00 160.0
Tomato Paste 40.0 320.0