Assignment:
1. Crew members attempt to escape from a damaged submarine 126 m below the surface. What force must be applied to a pop-out hatch, which is 1.43 m by 0.716 m, to push it out at that depth? Assume that the density of the ocean water is 1024 kg/m3 and the internal air pressure is at 1.00 atm.
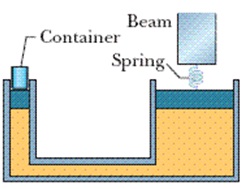
2. In the figure, a spring of spring constant 2.60 x 104 N/m is between a rigid beam and the output piston of a hydraulic lever. An empty container with negligible mass sits on the input piston. The input piston has area Ai, and the output piston has area 26.0Ai. Initially the spring is at its rest length. How many kilograms of sand must be (slowly) poured into the container to compress the spring by 7.70 cm?
3. A block of wood floats in fresh water with 0.799 of its volume V submerged and in oil with 0.931 V submerged. Find the density of (a) the wood and (b) the oil.
4. A hollow sphere of inner radius 8.69 cm and outer radius 9.76 cm floats half-submerged in a liquid of density 900.00 kg/m3. (a) What is the mass of the sphere? (b) Calculate the density of the material of which the sphere is made.
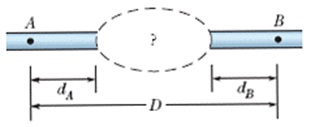
5. The figure shows two sections of an old pipe system that runs through a hill, with distances dA = dB = 31.0 m and D = 115 m. On each side of the hill, the pipe radius is 2.30 cm. However, the radius of the pipe inside the hill is no longer known.To determine it, hydraulic engineers first establish that water flows through the left and right sections at 2.30 m/s. Then they release a dye in the water at point A and find that it takes 98.0 s to reach point B. What is the average radius of the pipe within the hill?
6. Water is moving with a speed of 5.1 m/s through a pipe with a cross-sectional area of 3.8 cm2. The water gradually descends 11 m as the pipe increases to 9.3 cm2. (a) What is the speed at the lower level? (b) If the pressure at the upper level is 1.8 × 105 Pa, what is the pressure at the lower level?
7. In an electric shaver, the blade moves back and forth over a distance of 1.9 mm in simple harmonic motion, with frequency 124 Hz. Find (a) the amplitude, (b) the maximum blade speed, and (c) the magnitude of the maximum blade acceleration.
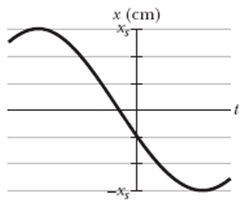
8. What is the phase constant (from 0 to 2π rad) for the harmonic oscillator with the position function x(t) given in the figure if the position function has the form x = xmcos(ωt + φ)? The vertical axis scale is set by xs = 7.50 cm.
9. An oscillator consists of a block attached to a spring (k = 412 N/m). At some time t, the position (measured from the system's equilibrium location), velocity, and acceleration of the block are x = 0.0935 m, v = -12.3 m/s, and a = -134 m/s2. Calculate (a) the frequency of oscillation, (b) the mass of the block, and (c) the amplitude of the motion.
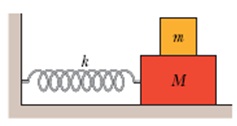
10. In the figure, two blocks (m = 1.90 kg and M = 9.50 kg) and a spring (k = 180 N/m) are arranged on a horizontal frictionless surface. The coefficient of static friction between the two blocks is 0.360. What amplitude of simple harmonic motion of the spring-blocks system puts the smaller block on the verge of slipping over the larger block?
11. A 17.8 kg object on a horizontal frictionless surface is attached to a spring with k = 1300 N/m. The object is displaced from equilibrium 35.7 cm horizontally and given an initial velocity of 12.7 m/s back toward the equilibrium position. What are (a) the motion's frequency, (b) the initial potential energy of the block-spring system, (c) the initial kinetic energy, and (d) the motion's amplitude?
12. A block of mass M = 5.00 kg, at rest on a horizontal frictionless table, is attached to a rigid support by a spring of constant k = 5830 N/m. A bullet of mass m = 8.40 g and velocity of magnitude 510 m/s strikes and is embedded in the block (the figure). Assuming the compression of the spring is negligible until the bullet is embedded, determine (a) the speed of the block immediately after the collision and (b) the amplitude of the resulting simple harmonic motion.
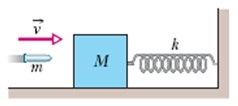
13. The pendulum in the figure consists of a uniform disk with radius r = 19.0 cm and mass 820 g attached to a uniform rod with length L = 480 mm and mass 300 g. (a) Calculate the rotational inertia of the pendulum about the pivot point. (b) What is the distance between the pivot point and the center of mass of the pendulum? (c) Calculate the period of oscillation.
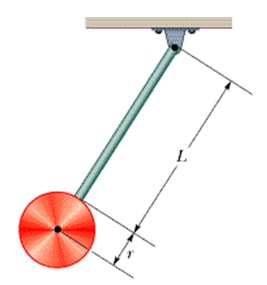
14. In the figure, a stick of length L = 1.2 m oscillates as a physical pendulum. (a) What value of distance x between the stick's center of mass and its pivot point O gives the least period?(b) What is that least period?
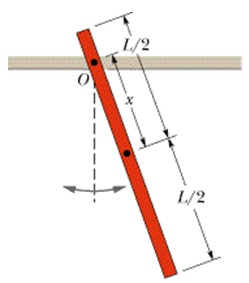
15. For a damped simple harmonic oscillator, the block has a mass of 1.4 kg and the spring constant is 11 N/m. The damping force is given by -b(dx/dt), where b = 190 g/s. The block is pulled down 12.1 cm and released. (a) Calculate the time required for the amplitude of the resulting oscillations to fall to 1/7 of its initial value. (b) How many oscillations are made by the block in this time?
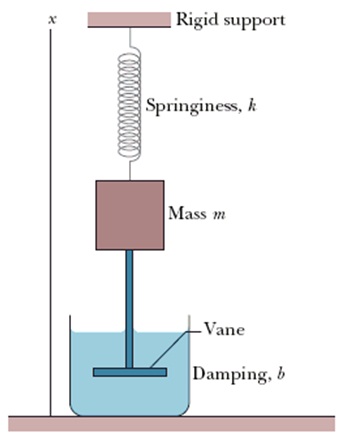
16. A 45.0 g block oscillates in SHM on the end of a spring with k = 1600 N/m according to x = xm cos(ωt + φ). Assume the block starts out moving in the -x direction. How long does the block take to move from position +0.800xm to (a) position +0.600xm and (b) position -0.800xm?
17. An engineer has an odd-shaped 10.1 kg object and needs to find its rotational inertia about an axis through its center of mass. The object is supported on a wire stretched along the desired axis. The wire has a torsion constant κ = 0.656 N•m. If this torsion pendulum oscillates through 19 cycles in 43.8 s, what is the rotational inertia of the object?
18. A block weighing 18.0 N is attached to the lower end of a vertical spring (k = 156.0 N/m), the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.50 J as it passes through the point at which the spring is unstretched.
(a) What is the period of the oscillation?
(b) Use the law of conservation of energy to determine the maximum distance the block moves above the point at which the spring is unstretched. (The maximum points above and below are not necessarily the same.)
(c) Use the law of conservation of energy to determine the maximum distance the block moves below the point at which the spring is unstretched.
(d) What is the amplitude of the oscillation?
(e) What is the maximum kinetic energy of the block as it oscillates?