Waste Management
City 1 produces 500 tons of waste per day, and city 2 produces 400 tons of waste per day. Waste must be incinerated at incinerator 1 or 2, and each incinerator can process up to 500 tons of waste per day. The cost to incinerate waste is $40/ton at incinerator 1 and $30/ton at incinerator 2. After incineration, the waste should be sent to a disposal landfill. The landfill will receive the 900 tons of incinerated waste per day (i.e., the waste produced will go through an incinerator then go to the landfill). It costs $3 per mile to transport a ton of material. Distances (in miles) between locations are shown in the table below.
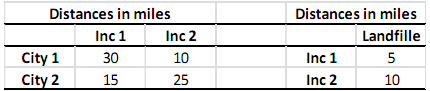
As the waste disposal planner, you want to minimize the total cost of shipping the waste produced in cities to disposal landfill after incineration. In this problem, you are asked to formulate the above waste disposal planning problem as a minimum cost flow problem.
a) Express the above problem on a network by drawing nodes, arcs, determining node values, arc costs, arc capacities if any, such that no node has a capacity restriction associated with it and no node has a cost for using the node. (Hint: How would you modify your network so that you do not have capacity constraints on your nodes and costs on your nodes?). Then, mathematically formulate the above problem as a minimum cost flow problem using the network representation that you have.
b) Formulate the problem you had in part a in Excel and solve it using excel solver.