Assignment:
Q1. To find the general integral of the differential equation y' = y/x = x2 + 1 , discuss existence et uniqueness and find the particular integral that passes for the point (1;5/2)
Q2. Considering the linear equation of the 2nd order
z’’ – (2/x) z’ + (2/ x2)z = 10 / x2 , x > 0 .
If we know that the functions:
y1(x) = 2x+5 , y2(x) = x2 +5 , y3(x) = x2 +2x+5
are solutions of the equation, write the general integral, justifying the procedure.
Q3. To find the general integral of the differential equation y'' - 3y' + 2y = xex
Q4. To calculate = ∫∫E (sin (3y) - x y2 + 2 ) dx dy
Where E is an ellipse with center in the origin and semi-axes with lenght 1 and 2, that has the cartesian axes as axis of simmetry, avoiding not necessary calculation.
Q5. To draw the integration’s domain and to exchange the order of integration of the following double integral, calculating the value:
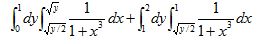
Q6. Calculate the following double integral ∫T Xdt where
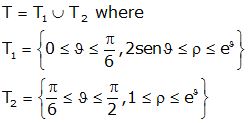
Q7. To calculate the curve integral of the function: f(x,y) = x2 – 2y2 alon the line OAB, where O(0,0), A(-2,1) B(1,1).
Q8) To consider the vector field V(x, y) = (V1, V2) = (( y2 – 1/x, 2xy + 1/y).
To verify that the field is conservative in the set A = {(x, y ) ∈ R2 : x > 0, y > 0 }.
To determine the potential function that is cancel out in (1, 1).
Provide complete and step by step solution for the question and show calculations and use formulas.