Assignment:
Let V be the space of all functions from R to R. It was stated in the discussion session that this is a vector space over R
Let F be a field, V a vector space over F, and v1,...,vk vectors in V. Prove that the set Span({v1, ..., vk}) is closed under scalar multiplication.
Q1. Label the following statements as true or false
a) The zero vector is a linear combination of any nonempty set of vectors
b) If S is a subset of a vector space V, then span (S) equals the intersection of all subspaces of V that contain S..
Q2. In each part, determine whether the given vector is in the span of S.
a)
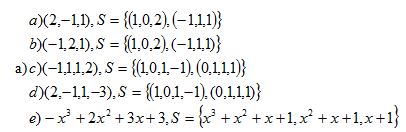
Q3. In F^n, let e denote the vector whose jth coordinate is 1 and whose other coordinates are 0. Prove that {e1,e2,…,en} generates F^n.
Q4. Label the following as true or false statements true or false.
a) If S is a linearly dependent set, then each vector in S is a linear combination of other vectors in S
b) Any set combination the zero vector is linearly dependent.
c) Subsets of linearly dependent sets are linearly dependent
d) Subsets od linearly independent sets are linearly independent.
Q5. In F^n, let e denote the vector whose jth coordinate is 1 and whose other coordinates are O. Prove that {e1, e2, …., en}is linearly independent.
Q6. Give an example of 3 linearly dependent vectors in R^3 such that none of the three is a multiply of another.
Provide complete and step by step solution for the question and show calculations and use formulas.