Questions:
Vandermonde Determinant Properties
Please show complete steps for the question on Vandermonde determinant properties attached.
Let x1,x2,x3, and x4 be real numbers.
(i) Compute the determinant of
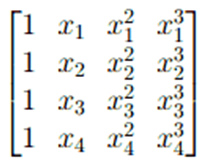
(ii) Explain briefly and concisely while the given matrix is nonsingular (invertible, or has inverse) if the real numbers x1, x2, x3 and x4 are distinct.
(iii) Explain why we can conclude from the preceding question, that through given four points (x1, y1), (x2, y2), (x3, y3), (x4, y4) on the plane with distinct abscissa x1, x2, x3 nd x4, we can draw exactly one cubic curve given by an equation y=ax3 + bx2 + cx + d, where a, b, c and d are real numbers.