Solve the linear System Ax =b using Gaussian Elimination.
a) Using matlab write the function [Bag,x] = EG(A,b) to solve the system without pivoting. The solution is the vector x and flag is 0 when the algorithm is completed and 1 otherwise.
b) Run with the following two linear systems:
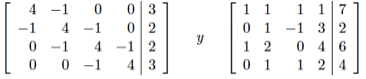
c) Using the tic and toc functions of matlab to estimate the time in the execution of the function of pan (a). Graph n versus time, Using systems of size n = 1000, 2000, 3000 and 4000.
d) Implement the algorithm of the part (a) to calculate the inverse of a function, using a function [B,flagpinverse(A), flag is 0 when is accomplished correctly and 1 otherwise. Run this code for find the inverse of the following matrix:
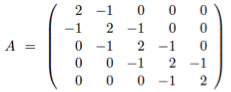
e) Now, solve the linear system Ax=b, where A is a Hilbert Matrix using the command hilb(n). Use the function of part (a) to solve this system for n 5,10,15,20 and bell^ is such that the exact solution is the vector xoeRa where all of his components are equal to 1. Show the results in a table using the format long e. Comment your results. Also, the command Mb in Matlab solves the system Ax=b, use this command to solve this to show the difference.