Type A problems
A1. If p : X -> X* is surjective and X is a topological space, show that the collection T = {V ⊂= X*: p-1(V) is open in X} is a topology (that's the quotient topology).
A2. If p : X-> X* is surjective, show that the quotient topology on X* is the finest topology for which p is continuous. That is, if T is any topology on X* in which p is continuous, then T is contained in the quotient topology.
A3. Give an example of a Hausdorff space X and a surjective map p : X-> X*so that the quotient space X* is not Hausdorff.
A4. Let X be a topological space, p : X-> Y and q : Y ->Z surjections. Give Y the quotient topology induced by p. Then Z can be given the quotient topologies induced by q or by q ° p. Show that these topologies are the same.
A5. Consider the function p : R ->{a, b, c} given by:
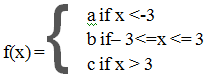
List the open sets in the quotient topology on {a, b, c}.
A6. Let X be a hexagon in the plane with the relative topology from R2 (interior of the hexagon is included). Identify opposite sides of the hexagon with identifcation (arrows) occuring in same direction. What is the resulting space?
Type B problems
B1.Let a surjectivep : X -> X* induce the quotient topology on X*. Give an example
where p is not an open map and one where p is not a closed map (open, closed maps send open sets to open sets or closed sets to closed sets, respectively).
B3. Let D2 be the unit disk {(x1,x2) ∈R2: x11+ x22<=1} with the relative topology fromR2. Define an equivalence relation: x ~ y if x12+x22= y12+y22. Identify the familiar quotient space given by this relation and then show precisely that the quotient topology on this space is the same as the usual one.
B6.Show by induction on g that a genus-g surface with k crosscaps is homeomorphic to the sphere with k + 2g crosscaps.