Questions:
Trigonometry - Heights and Distances
1. The following chart shows some common angles with their degrees and radian measures. Fill in the missing blanks by using the conversions between radians and degrees to find your solutions. Show all work to receive full credit.
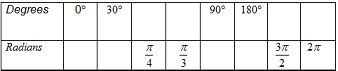
2. Two boats leave the port at the same time. The first boat travels due east at 14 mph, and the second boat travels at 28 mph in the direction of .
To the nearest tenth of a mile, how far apart will the boats be in a half an hour? (Hint: Distance = (Rate)(Time), 0.5 represents a half an hour.)
3. Use common trigonometric identities for the functions given to find the indicated trigonometric functions. (Hint: Remember the reciprocal properties of sine, cosine, and tangent.) Show all work to receive full credit. Give answers in exact form - no decimals.
A. If sin 30o = 1/2 and cos 30o = √3/2,what are the value of
a) tan 30o =
b) Csc 30o =
c) cot 30o =
B. If sec Θ = 3 and tan Θ = 2√2, what are the values of
a) cot Θ
b) sin Θ =
c) cos2Θ =
4. Solve the following application problem. Show all work to receive full credit.
A. A man at ground level measures the angle of elevation to the top of a building to be 53o . If, at this point, he is 12 feet from the building, what is the height of the building? Draw a picture, show all work, and find the solution. Round to the nearest hundredths.
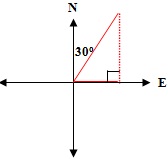
B. The same man now stands atop a building. He measures the angle of elevation to the building across the street to be and the angle of depression (to the base of the building) to be .
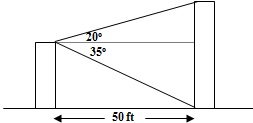
If the two buildings are 50 feet apart, how tall is the taller building? See the figure. Round to the nearest hundredths.
5. A weather balloon B lies directly over a 1000-meter airstrip extending from A to C.
The angle of elevation from A to B is and from C to B is (Larson, Hostetler, & Edwards, 2005).
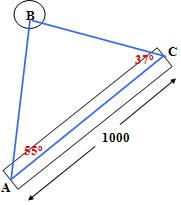
Find the distances from A to B and from C to B. Show all work to receive full credit. Round to the nearest hundredths.