Transshipment problem as a linear-programming model

Question

Problems:

Question:

DSS Inc. is an electronics company with production facilities located in Atlanta, Boston, and Chicago. Components produced at these facilities may be shipped to the firm's regional warehouses that are located in Edison and Fargo. From the warehouses the firm supplies retail outlets located in Houston, Indianapolis, and Jacksonville.

The capacity of each production facility is presented below:

Atlanta	Boston	Chicago
800	500	700

The firm must meet the demands specified below for each retail outlet:

Houston	Indianapolis	Jacksonville
900	600	500

The transportation cost per unit from each facility to each warehouse is specified below:

	Atlanta	Boston	Chicago
Edison	6	1	3
Fargo	4	8	1

The transportation cost per unit from each warehouse to each retail outlet is specified below:

	Houston	Indianapolis	Jacksonville
Edison	8	3	4
Fargo	2	3	8

The firm has to determine an optimal transshipment plan that minimizes total transportation cost while meeting the demands in each retail outlet and not exceeding the capacity at each production facility.

(a) Formulate the transshipment problem as a Linear-programming model and determine the optimal transshipment plan.

(b) In the analysis so far we have ignored the cost of operating each warehouse. If a warehouse is operated, a fixed cost must be incurred. If a warehouse is not operated, the fixed cost can be avoided but no shipment can occur through that warehouse. ). The fixed costs for warehouse operation are given below:

	Cost
Edison	$10,000
Fargo	$5,000

 

 

Determine the optimal plan that minimizes the total cost (total cost is defined as the sum of the cost of transportation and the cost warehouse operation).

My partial Answer:

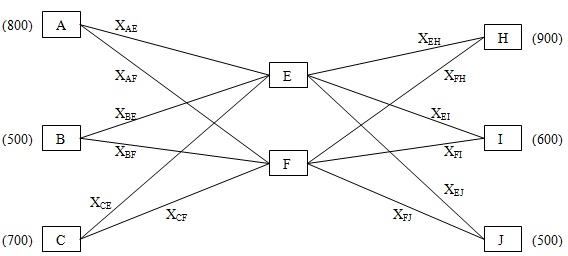
X_AE , X_AF , X_BE  , X_BF , X_CE , X_CF , X_EH , X_FH , X_EI , X_FI , X_EJ , X_FJ

Capacity Constrains:

X_AE + X_AF ≤ 800

X_BE + X_BF ≤ 500

X_CE + X_CF ≤ 700

Demand Constrains:

X_EH + X_FH ≤ 900

X_EI + X_FI ≤ 600

X_EJ + X_FJ ≤ 500

X_AE + X_BE + X_CE = X_EH + X_EI + X_EJ

X_AF + X_BF + X_CF = X_FH + X_FI + X_FJ

Objective Function:

Minimize the cost = 6X_AE + 4X_AF + X_BE + 8X_BF + 3X_CE + X_CF + 8X_EH + 2X_FH + 3X_EI + 3X_FI + 4X_EJ + 8X_FJ

b) Three options:

Keep both warehouses open: add operating cost of $15000

Close Fargo: add operating cost of $10000

Close Edison: add operating cost of $5000