The unit impulse response of the system - find the first

Question

Part -1:

1. You are given a spherically symmetric volume charge distribution located in free space, with ρ = 3r² for r < a, and ρ = 0 for r > a.

(a) Use Φ(r) = 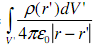to calculate the potential at the center of the charge distribution.

(b) Now calculate the electric field E from Gauss' law and then obtain the potential at the center of the charge distribution by evaluating

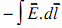where the limits range from ∞ to 0.

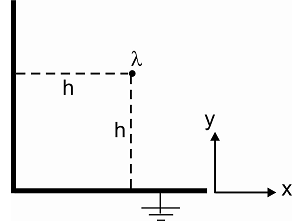
2. Consider a thin wire carrying a uniform charge per unit length of λ (C/cm), and placed near two conducting planes, as shown. Calculate the magnitude and direction of the electrical force on unit length of wire.

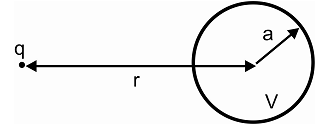
3. Consider a point charge q at distance r from a conducting sphere of radius a. The sphere is at potential V. Find the value and the location of the two charges that, when placed within the region occupied by the sphere, will, together with the external point charge q, produce potential V at the surface of the sphere and a potential Φ that satisfies Poisson's equation in the region outside the sphere.

Part -2:

Q1 Find the first three terms of the causal signal f [k] (that is, find f [0], f [1] and f [2]) if

F[z] = 3x³ + 13z² + z / z³ + 7z² + 2z + 1

Find your answer by expanding F[x] as a power series in z^-1.

Q2 Using the 2-transform, solve

y[k + 1] + 2y[k] = f[k + 1]

with y[0] = 1 and f [k] = 3^-(k-1) u[k].

Q3 Using the Z-transform, solve

y[k + 2] + 2y[k + 1] + y[k] = f [k]

with y[-1] = 1, y[-2] = 0, and f [k] = u[k]

Note:

kγ^kU[k] <=> γz/ (z - γ)²

Q4 Using the z-transform, find h[k], the unit impulse response of the system described by the following equation:

y[k+ 2] + 2y [k + 1] + y[k] = 2f [k + 2] - f [k + 1]