The slopes in the direction field are all identical along

Question

The Phase Line

Sketching the direction field of a differential equation dy/dt = f(t, y) is particularly easy when the equation is autonomous-that is, the independent variable t does not appear expelicitly

- dy/dt = f(y) .

In Figure 1.17(a) the graph exhibits the direction field for -y' = -A(y- y₁)(y-y₁) (y - y₂)² and A > 0. and some solutions are sketched. Note the following properties of the graphs and explain how they follow from the fact that the equation is autonomous:

(a) The slopes in the direction field are all identical along horizontal lines.

(b) New solutions can be generated from old ones by time shifting (i.e., replacing y(t) with y(t - t₀).

From observation (a) it follows that the entire direction field can be described by a single direction "line," as in Figure 1.17(b).

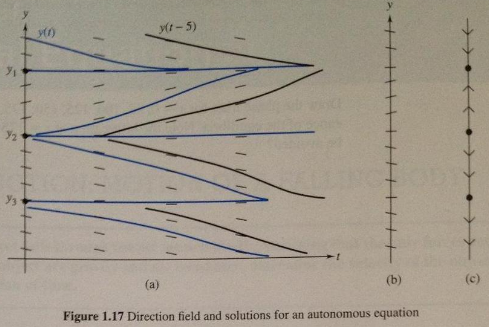
Figure 1.17 Direction field and solutions for an autonomous equation

Of particular interest for autonomous equations are the constant, or equilibrium, solutions y(t) = y_i, i = 1, 2, 3. The equilibrium y = y_i is called a stable equilibrium, or sink, because the neighboring solutions are attracted to it as I -->oo. Equilibria that repel neighboring solutions, like y = y₂, are known as sources; all other equilibria are called nodes, illustrated by y = y₃. Sources and nodes are unstable equilibria.

Attachment:- project.jpg