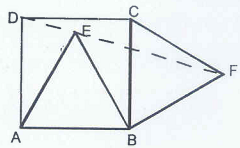
1) On sides AB and BC of square ABCD equilateral triangles ABE and BCF are constructed as shown. Prove that points D, E, and F are collinear.
2) In right triangle ABC with the right angle at C, CH is an altitude and AC = AM. Prove that ∠1 = ∠2.
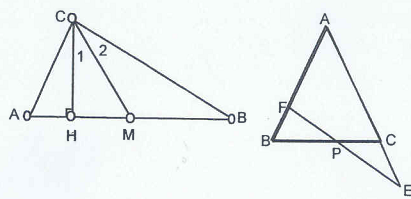
3) In isosceles triangle ABC [AB = AC] P is an arbitrary point on base BC and E is on the extension of side AC so that CE = CP. Prove that ∠AFE = 3∠AEF.
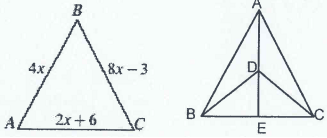
4) The lengths of the sides of a triangle are 2x + 6, 4x, and 8x - 3. For what values of x is this triangle isosceles? Justify your answer.
Attachment:- geometry.pdf