Steady state two dimensional seepage problem

Question

Assignment Problem:

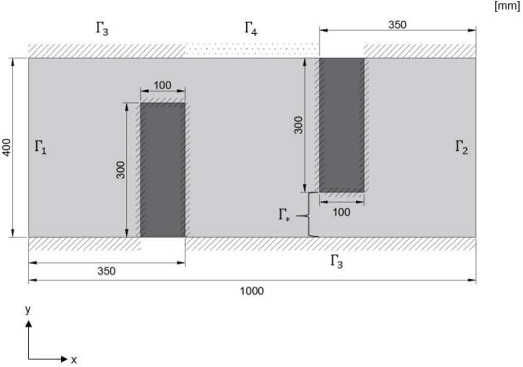
Consider a steady state two dimensional seepage problem as shown above. There are four different kinds of the boundary conditions in this problem. The pressure value is prescribed on Γ₁, and Γ₂; PΓ₁ = 100 kPa, PΓ₂ = 150 kPa. Γ₃ is an impermeable surface, i.e. the flux in the normal direction to the surface is zero. Γ₄ is a partially permeable so that the flux to the surface is given by J = 1 x 10^-4 e m/s

The hydraulic conductivity of the porous medium is k = 4.2 x 10^-6 m/s.

The governing equation of this problem is given by a Laplace equation, i.e.

2P = ∂²P/∂x² + ∂²P/∂y² = 0

Subjected to

P = P₀ on Γ₀ (Dirichlet condition)

-k∂P/∂n = Jn on Γ_J  (Neumann condition)

Q1. Investigate the problem and build a plan for the numerical analysis.

Q2. Build the solution procedure.

Q3. Solve the system and consider to the following questions.

- Provide the pressure field.

- Calculate the amount of water passing throughout Γ* in an hour. (Approximate the thickness = 1m)

- Provide the field of the maximum flux, i.e.

J_x = -k.∂P/∂_x, J_y = -k.∂P/∂y

J = √(Jx² + Jy²)

Q4. Discuss your result.

Use your own linear algebraic solver.

Avail our Steady State Two Dimensional Seepage Assignment Help service and put a full stop to sleepless nights and low academic grades at affordable prices!

Tags: Steady State Two Dimensional Seepage Assignment Help, Steady State Two Dimensional Seepage Homework Help, Steady State Two Dimensional Seepage Coursework, Steady State Two Dimensional Seepage Solved Assignments, Dirichlet Condition Assignment Help, Dirichlet Condition Homework Help, Neumann Condition Assignment Help, Neumann Condition Homework Help