Question 1. You live in country "I-love-spring-and-gosh-I-wish-I-could-go-outside-now" (ILSAG, for short). ILSAG has a Cobb Douglass production function Y=K1/2L1/2. The hard-working citizens of ILSAG save 20% of their incomes and the depreciation rate in the economy is 10%.
a. According to the Solow model, what should be the steady-state level of capital per worker?
b. What would be the "golden rule" level of capital per worker?
c. What savings rate would give rise to the golden rule level of capital?
d. Suppose you are the almighty ruler of ILSAG and your dutiful citizens do everything you tell them. If you care only about your citizens long-run happiness (read: consumption) what fraction of their savings should you have your citizens save?
e. Given your last answer, suppose that you tell your people to switch their initial savings rate from what it was initially to the rate that would make them happiest in the long-run. What will be the dynamics of the capital stock in the short run?
f. What will be the dynamics of the capital stock in the long run?
g. How will the consumption level of a typical citizen evolve over time? h. Finally, suppose that while your citizens like you, they don't like you that much. Could you see any problem in implementing the policy just suggested?
Question 2. Suppose you are given the production functionY = F(K, L) = AK1/4L3/4 , where Y is real GDP, K capital, L labor and A technology.
a. Suppose K and L are both doubled in this economy. Does this production function exhibit constant returns to scale? Provide a proof of your answer.
b. Rewrite the above production function in terms of output per worker, y. That is, normalize the function so that it can be written as y = f(k) where k is capital per worker. Provide a verbal interpretation of your mathematical result.
c. Using the expression you found in part (b) and assuming labor is equal to 16 units, fill in the following table. Recall that k, the capital to labor ratio (K/L), measures capital intensity: that is, it provides a measure of how much capital each unit of labor has to work with in the economy. Assume that A equals 2 in this problem. Hint: this might be a good time to pull out your Excel spreadsheet program.
L K k = K/L y = Y/L Y MPK
16 0
16 20
16 40
16 60
16 80
d. Use Excel to graph k and y, placing k on the horizontal axis and y on the vertical axis.
e. Let's define s as the saving rate per worker, i as the amount of investment per worker, and c as consumption per worker. Suppose that you are told that the saving rate in this economy is constant and equal to .25.
Use this saving rate and the values you found in part (c) to fill in the following table. Note that i equals sy and y = c + i.
L K k = K/L y = Y/L s I c
16 0
16 20
16 40
16 60
16 80
f. Suppose you are also told that depreciation of the capital stock, δ, is equal to 10% each year. Using this information, plus the information you have previously been given or have calculated compute the change in the capital intensity, ?k, in this economy. Find ?k for each level of K in the economy by filling in the table below. Recall that the change in the capital intensity is equal to the difference between the level of investment per worker and the amount of capital per worker that depreciates during the given time period.
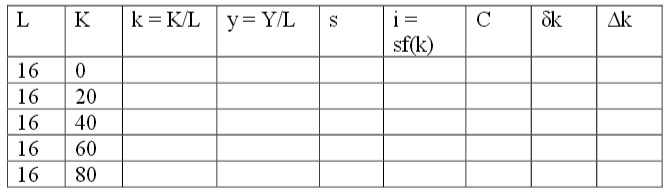
g. Now, graph the amount of depreciation, δk; the level of investment per worker, i (which is also equal to sf(k)); and the capital intensity, k. Place k on the horizontal axis and δk and sf(k) on the vertical axis.
h.Suppose we define k* as the steady-state level of capital intensity or the level of capital per worker where the amount of capital depreciation per worker equals the level of investment per worker in each period. At k* the capital intensity is constant over time. Calculate the value of k* for your economy. Does your calculation agree with your findings in part (g)?
i. What would happen to k* if s increased, holding everything else constant? Draw a sketch illustrating the initial situation and the effect of an increase in s. [Hint: why not run your Excel program again but this time with a higher value for s?]j.What would happen to k* if δ increased, holding everything else constant? Draw a sketch illustrating the initial situation and the effect of an increase in δ. [Hint: why not run your Excel program again but this time with a higher value for δ?]