Solving systems of equations using gaussian elimination

Question

Assignment:

Q1. Let P (n) be the statement that 1³+ 2³+···+ n³=(n(n+ 1)/2)² for the positive integer n.

a) What is the statement P (1)?

b) Show that P (1) is true, completing the basis step of the proof.

c) What is the inductive hypothesis?

d) What do you need to prove in the inductive step?

e) Complete the inductive step, identifying where you use the inductive hypothesis.

f)   Explain why these steps show that this formula is true whenever n is a positive integer.

Q2. Show all work .Solve the following systems of equations using Gaussian Elimination.Your procedure should be in matrix form.

x₁ + x₂ + x₃= 1

2x₁ - x₂ + x₃= 2

-1x₂ + x₃= 1

Q3. Determine the solutions of the system of equations whose matrix is row equivalent to

Give three examples of the solutions. Verify that your solutions satisfy the original system of equations.

Q4. Solve for

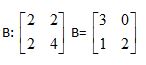
Provide complete and step by step solution for the question and show calculations and use formulas.