Problem:
Solving system of differential equations and eigenvalues
1) The slope field for the system
dx/dt = 2x + 6y
dy/dt = 2x - 2y
Is shown below
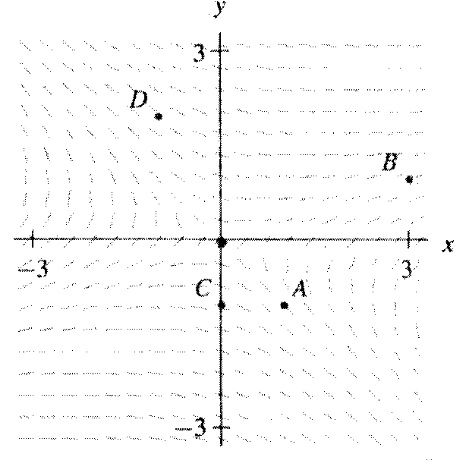
a) Determine the type of the equilibrium point at the origin.
b) Calculate all straight-line solution.
2) Show that a matrix of the form A = ( a b) with b≠0 must have complex eigenvalues.
(-b a)
3) Let A→ = ( a b) → Define the trace of A→to be tr ( A→ ) = a + d. Show that A→ has only one eigennvalue.
( c d )
If and only if ( tr ( A→))2 -4 det (A→) = 0