Assignment:
A local post office plans the route of its letter carrier. The region has eight street junctions and twelve street segments, which the carrier has to serve. Figure shows the streets and the junctions as well as the distances (in hundreds of feet).
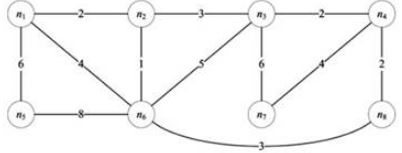
(a) Is it possible for the post office to find a tour for the postman, so that the letter carrier has to traverse each street exactly once?
(b) In case a tour as sought under (a) does not exist, determine a tour that minimizes the total distance that the letter carrier has to walk. What is the length of such a tour?
(c) The agreement with the letter carriers’ union stipulates that the post office has to pay $2 per ft and year to the letter carrier. It has now become possible to hire an outside firm for the service. However, there are two individuals who agree to do the job, but only if they can split the tour among themselves in a specific way, as each has a preference for certain neighbourhoods. In particular, Joe, the first potential carrier, would like to cover the streets e12, e15, e23, e26, e34, e37, and e48, while Jim, our second carrier, prefers to deliver the mail along the remaining streets. How much can the post office offer them, if they do not want to pay more than they do for a single carrier under the present system?
Provide complete and step by step solution for the question and show calculations and use formulas.