Question:
Solution of the equation of motion of a spring mass system
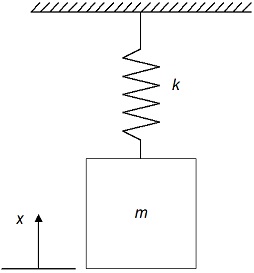
A certain engineering system can be represented by mass in a spring. If the mass is pulled downwards and then released, it oscillates on the spring. Using Newton's second law, a homogeneous second-order differential equation can be set up as below:
m d2x/dt2 + kx = 0
If the mass m is 1kg and the spring's stiffness k is 100N/m, find an expression for the displacement x with respect to time t, when t=0, x(0)=0 and x`(0)=1