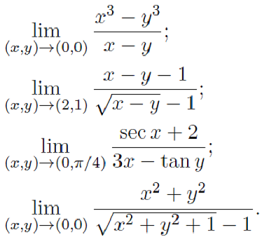Problem 1: Consider the function f (x, y) = xy + 2. Draw the level sets {f = c} for c = 1, 2, 3. On the same graph, sketch the gradient vector fields ∇f at the points (0, -1), (1, 1), and (-1, 1). [Point to ponder: what is the shape of the graph of f?]
Problem 2: Assume that the x-axis runs west to east and the y-axis runs south to north. Assume that the temperature on a stove is described by the following function:
Θ(x, y) = 1.5y + y/(x2+1) + 100.
Throughout, x and y are measured in centimeter, and Θ is measured in Celsius.
(1) A bug at (1, -2) is crawling southeast at the speed 4 cm/ sec. How fast is the temperature experienced by the bug changing?
(2) If this bug wanted to move in the direction in which the temperature decreases the fastest, in which direction should it crawl?
Problem 3: Evaluate ∂xxzzyxzxyzxxzxzxyF for
F(x, y, z) = y2ezcosx/(1+x4z3+arctan(x2+z2)),
and justify your answer.
Problem 4: Assume that a particle moves in R3 with velocity
v(t) = 3te4^2i - (1/(√t+3))j + sin(3t)k,
and that it passes through the point (3/2, 2, 0) at time t = 0. Find its acceleration (as a function of t) for t ∈ [0; 2], and determine its position at t = 1.
Problem 5: Consider the surface S ⊂ R3 given by equitation z = x2 + 2xy-y+2019. Find all points (xo, yo) at each of which the tangent plane of S in parallel to the (x,y)-plane.
Problem 6: The following functions f are all defined on the whole plane R2. Determine the largest possible set in each case on which f is continuous. Justify your answer.
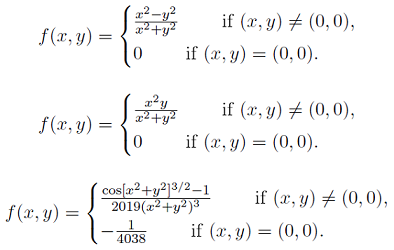
Problem 7: Evaluate the following limits: