Sketch a phase diagram corresponding to each of these cases

Question

1. The general form of a Lienard system is

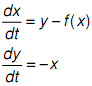
If  f(x) = μ(x³ - x), this is the system form of Van der Pol's equation. Find all the equilibria of the Van der Pol equation and characterize them as sources, sinks, etc. Make sure to analyze the influence of µ on the characterization.

2. Komarova and co-workers have devised a simple 2-D dynamical system model of cell dynamics in bone remodeling. The equations associated with their model are:

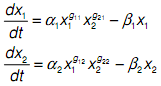
Here, we're interested only in positive values of x₁ and x₂, β₁ > 0 and β₂ > 0, and the parameters g_ij may take on any real values.

Find all equilibria (again, we're only interested in the first quadrant) of the system. Identify degenerate cases. Find values of the parameters for which at least one of the equilibria is a source, other values for which at least one is a sink, others for which at least one is a saddle, others that yield a center, others that yield a stable focus, and others that yield an unstable focus.

Sketch a phase diagram corresponding to each of these cases. Try to make some general statements about the structure of equilibrium as a function of the parameters.

Attachment:- dy-pdf.pdf