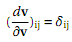1. THE VLASOV EQUATION
Show that the one-dimensional Vlasov equation,
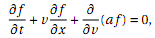
can be obtained by Taylor expansion of the right-hand side of:
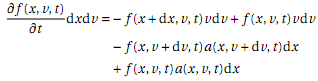
2. ISOTROPIC PRESSURE
Show that the off-diagonal terms of the pressure tensor
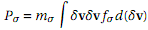
vanish if f¾ is an isotropic function of ±v (i.e., randomization is the same in any direction). Hint: Expand the the tensor ±v ¢±vf¾ and integrate terms individually (you need only do this for one diagnoal term, and one off-diagona, and argue similarity with other tensor terms).
3. ACCELERATION TERM IN THE VLASOV EQUATION
Show that the acceleration integral in the ?rstmoment of the Vlasov equation gives
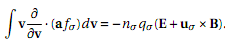
Hint: Integrate by parts, taking into account that