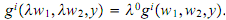questionconsider a firm which produces a good y

Question

Question:

Consider a firm which produces a good, y, using two inputs or factors of production, x1 and x2.Thefirm's production function is

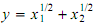
The firm faces exogenously given factor prices, w1 and w2.Thefirm's total cost of production, TC, is

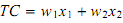
For any given level of output y, the firm wishes to choose the levels of x1 and x2 which minimize the cost of producing that level of output. That is, the firm wishes to minimize (2) by choice of x₁ and x₂ subject to the constraint given by (1).

(a) Write down the Lagrangean function associated with this problem.

(b) Derive the first-order conditions for this problem.

(c) Solve the first-order conditions for x₁ and x₂ as functions of w₁, w₂, and y. That is, derive expressions of the form

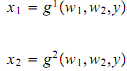
These functions are known as conditional factor demand functions, since they express the demand for x₁ and x₂ as a function of factor prices, conditional on producing a given level of output, y.

(d) How does the cost minimizing ratio of x1 and x2 change as the level of output changes? Briefly explain.

(e) Afirm's cost function, which we denote by c(w1,w2, y), expresses total cost as a function of the level of output and factor prices.Show that the firm's cost function may be written as

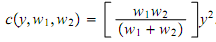
(f) Show that

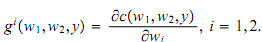
e) differentiating (3) with respect to the ith factor price. This result is known as Shephard's Lemma.(g) A function

y = f(x₁, x₂)

is said to be " homogeneous of degree k"if

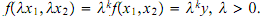
That is, when both x1 and x2 are increased by a factor, y increases by a factor k.

i) Prove that the production function given by (1) is homogeneous of degree 0.5 in x1 and x2.

ii) Prove that the conditional demand functions for x1 and x2 derived in part (c) are homogeneous of degree zero in w1 and w2. That is, prove that